Public Transport and Infectious Diseases

This is a rough set of guidelines for how to make public transport networks more resilient to infectious diseases. While this post is inspired by the Covid-19 pandemic, some of what I’m going to discuss here is relevant to infections in general, both seasonal flu and future generational epidemics.

I’m aiming mainly at people who work for public transport authorities and can act to epidemic-proof their systems in the future, but some of the guidelines may be helpful for riders. The key takeaway is that public officials probably should not want to shut down the system or discourage people from riding it; thus, as a rider you probably shouldn’t avoid the trains except insofar that you should avoid most places you’d take them to, like crowded offices and events.

Finally, let me be clear: my expertise on public health approaches zero. I have a fair amount of general knowledge of how different urban rail systems operate, but more about network design and costs than public health. To the extent I’m ahead of anyone else on this issue, it’s that I’ve seen so much wanton incuriosity in the West (especially the US) toward Asian practices, and therefore asked around for East Asian practices rather than trying to learn worst industry practices from Europe and North America.

The scope of this post

The scope of what best industry practices are on epidemic prevention is, roughly, the high-income major cities of East Asia, plus Singapore. China is excluded on purpose: a country that arrests doctors for telling the public about the coronavirus isn’t really where you want to get disease prevention tips from. Instead, the low infection rates so far in Taiwan, Hong Kong, and Singapore, and South Korea’s ability to control the infection through mass testing after the explosion in cases at the Shincheonji church, suggest that those countries should be the models. Japan may be a good example as well, but the state is undertesting, so the full extent, while apparently lower than in Western countries, may be understated.

I have talked to people in Singapore, Hong Kong, and Seoul to understand the situation on the ground there. In Taipei and the cities of Japan I have not, and am relying on media report; I know I have commenters who live in Japan, so if you have anything to say about the efforts there then please do speak up and contribute, regarding both the measures taken and current infection rates.

This is necessarily a volatile situation. It’s possible that in a month, Germany and France will have controlled the infection while the rich countries of Asia will look as dire as Lombardy looks right now. I don’t think such an inversion is at all likely, but ultimately, I am describing the best information available as of 2020-3-11.

Do people need to stop taking mass transit?

Probably not. I emphasize probably because the different in-scope cities are reacting differently, and we don’t yet know for certain whether avoiding the trains is correlated with greater safety from infection.

In Singapore, life goes on. I have family there; I’m told that the MRT is not less crowded than the usual at rush hour, but the buses are definitely less crowded. The estimate I heard is that 1/3 to 1/2 of the population on the street is wearing surgical masks. Instead of shutting down schools and offices, the state imposed a mandatory quarantine on people arriving from early-infected countries including China, and went as far as revoking the green card of a permanent resident who violated the quarantine.

Update 2020-3-12: my sibling reports that, first, the mask-wearers are largely Chinese, not ethnic minorities like Malays and Indians, and second, ridership on the MRT is noticeably down at rush hour, with some empty seats where normally trains are standing-room only.

In Hong Kong, it is exactly the opposite. The state is not terribly relevant – the population does not trust it. There was early caution due to social memory of SARS, leading to rapid social distancing, closing down schools, offices, and public events. I’ve asked Lyman Stone and Trey Menefee for their impressions. They both said the MTR is empty nowadays, and Lyman reminded me that ridership was down even before the epidemic on account of a popular boycott in response to the company’s collaboration with regime security. The total social distancing means people travel little, but when they do, it’s often by TNC, leading to a lot of Uber traffic; drivers even put hand sanitizer in the back of their cars and make an effort to clean the interior well, to attract passengers afraid of catching the disease.

In Seoul, the situation is different, in that there was a big flare of the epidemic thanks to the so-called patient 31, a member of Shincheonji, who transmitted the virus around the group. Until a few days ago, Korea was the #2 country in the world in confirmed cases, after China, but Italy and Iran have since overtaken it and the US is poised to overtake it soon too. But new infections are down thanks to an aggressive regime of testing. Public transportation is still in operation – Min-Jae Park, an NYU student from Korea who has been working with me and Eric Goldwyn on our construction costs project, said that there is noticeably less ridership according to family but also,

Yesterday, there has been a group of confirmed cases in a same workplace including commuters via transit to and from Seoul. The government did declare that it is almost impossible track back individual patients to show if transit is a hazardous environment. However, since the early stages, the national and local  transit authorities has been aggressively sanitized the public realm especially in transit. Additionally, the ridership of the transit decreased overall, as the remote working culture started to become naturalized.

So far, there has not been a substantial case that proves that transit needs to be reduced or shut down, but we shall see how the yesterday’s case turns out. I will update to you if any policy change comes up relating to the virus, but I think that is probably the last thing the government want to do in scale of national lockdown Italy did.

My other source on Korea’s response is Nick Plott, a.k.a. Tasteless, a popular esports caster. In a short video about the virus and its effect on esports, he mentions the effect on Korea, and says that public transport in Seoul is deserted. My hunch is that Min-Jae’s take, although second-hand, is more accurate than Tasteless’s, and public transport in Seoul still has a fair amount of ridership, if not nearly so much as before the pandemic.

Update 2020-3-12: Min-Jae clarifies that as of the morning of the 13th Korea time, there is a shift to private transport even though the government says public transport is safe; he guesses ridership is down 20-30%.

In the big cities of Japan, ridership is down, though not by much relative to the magnitude of the crisis. The media quotes 10-20% declines in ridership on the Yamanote Line and on lines around Osaka, and 20-30% declines in ridership on the Nagoya subway. Maciej Ceglowski is visiting Japan and reports that the trains in Kyoto “are not crowded at all,” adding that about 3/4 of the people wear masks. Japanese office culture is resistant to working from home, as is I think office culture elsewhere in Asia-Pacific, and this has hampered social distancing efforts.

Finally, in Taipei, I do not have any information regarding public transport usage during the pandemic. That said, some circumstantial evidence that it is still going on is that the region has just opened a new circumferential line, the Yellow Line, and even let passengers ride for free for the first month, getting more than a million riders in 25 days, which is low but not outrageously so for a new circumferential line.

How can mass transit be made less infectious in the future?

There are two ways passengers can infect other passengers in public. The first is directly, through coughing, sneezing, or casual touching combined with touching one’s own face. The second is through intermediate surfaces, called fomites in epidemiology, such as poles, seats, door handles. Neither disease vector can be eliminated, but there are design elements that can greatly reduce both.

Infrared sensors for temperature checks

It’s possible to take people’s temperatures passively using infrared sensors. Taipei installed such sensors at one MRT station and is about to do so at six additional central stations. People with fever above 38 degrees will not be allowed into the station, and people with temperature between 37.5 and 38 degrees will have to undergo an ear temperature check to confirm that they do not have a fever. I saw this system at the airport when I visited Taipei three months ago, where it was used to screen passengers with fever.

This system requires all station entrances to be staffed. This may be expensive in smaller cities, but as a temporary measure during an epidemic, it’s fully justified. If you’re the government, you can afford to bust the budget in an emergency to make sure people can travel around the city without contracting a fatal disease.

Temperature checks will miss asymptomatic cases, but this is fine. The epidemiologist-turned-data-scientist Maria Ma summarizes the best available research on Covid-19: while asymptomatic transmission is possible, it requires much closer contact than being together on a train.

Hand sanitizer

Every station entrance should have hand sanitizer in sufficient quantities for the expected passenger traffic. Some office and university buildings already have this solution, even in the West; this is especially common in Singapore. My recollection of Taipei is that it had hand sanitizer at stations even in December, but I am not completely certain this was from Taipei and not Singapore or Bangkok.

Fomite reduction

Seoul offers disposable chopsticks for pressing elevator buttons. In the short run, transit agencies that use button-operated doors, such as those of Berlin and Paris, should do the same at stations and inside train cars, space permitting. In the long run, European agencies should be more like Asian (or North American) ones and have automatic doors opening at every stop.

In the long run, it’s also beneficial to design train interiors to inhibit the spread of viruses and bacteria. Some materials catch bacterial and viral infections more than others – for example, a 2015 study by Biranjia-Hurdoyal, Deerpaul and Permal finds that synthetic purses have far more bacteria than leather or cloth ones; this should be equally true of train seats. Moreover, the poles should be coated with copper, as it has biocidal and antiviral properties – a 2013 study by Salgado et al finds that coating ER surfaces with copper reduces the risk hospital-acquired infections, from 12.3% to 7.1% when all infections are included or from 8.1% to 3.4% excluding MRSA and VRE.

Fare barriers and station entrances should be designed to minimize fomites. The best option here is not used in Asia: no fare barriers at all, with proof-of-payment fare enforcement. But the smartcard systems and automatic fare barriers so common around Asia are a good second best, as they do not involve physical contact with foreign objects. The worst options are metal turnstiles that passengers turn with their hands, cage-style turnstiles, or heavy doors that passengers must push on their way out; these are found in New York and Paris, and should be replaced to reduce the spread of disease in the future.

Regular cleaning

Transport companies should clean their vehicles and stations regularly. This may not be realistic at bus stops, but is realistic on buses and trains and at all train stations. That ten-year-old piece of gum stuck to the floor of your New York subway station is not by itself a vector for a virus that only spread to humans three months ago, but if it’s still there, then so is the tissue thrown yesterday by someone who just got sick.

Seoul is using drones to spray disinfectant on hard-to-reach surfaces, such as playgrounds. This can also be used at railyards and elevated rail stations to speed up the process.

Employee safety

The guidelines above are designed for passenger safety. What about employee safety? This, I believe, is a smaller problem, at least in countries that are advanced enough to have good sick leave. It is notable that even in Hong Kong, trains are running, albeit the buses run at lower frequency as people are staying home.

A train driver works sitting alone in a cab separated from where passengers are is not at great risk, and neither is a bus driver separated by a glass screen. There is risk of worker-to-worker infection, especially if drop-in crews are common to control turnaround times, but it’s easier to test workers for fever and send sick ones home with pay than to deploy infrared sensors at every station entrance. As an additional layer of safety on top of temperature checks and generous sick leave, agencies should clean train and bus driver cabs between every crew change.

It’s workers who are together all the time who should not be going to work – that is, the head office. Planners, schedulers, managers, and clerical workers can work remotely, albeit at reduced productivity. Making regular plans to reduce infections during flu season, and planning how to respond to bigger epidemic threats in advance, is therefore useful since it doesn’t stress planning capacity at a time when productivity is the lowest.

What Europe Can Learn From Asia

Most of what I write about is what North America can learn from Europe, but the rich countries of Asia are extremely important as well. But what’s more interesting is knowledge sharing between Western Europe and the rich countries of East Asia. These two centers of passenger rail technology have some reciprocal exchange programs, but still learn less from each other than they should.

The ongoing coronavirus outbreak made the topic of Western learning from East Asia especially important. To be clear, none of the examples I’m going to talk about in this post is about the virus itself or at all about public health. But the sort of reaction in democratic East Asia that’s staved off the infection, compared with the failure of the West to do much in time, is instructive. When the virus was just in China, nobody in the West cared. I went to a comedy night in Berlin a month ago and it was the Asian comic who joked about how all they needed was to cough and the white people gave them space; it was still viewed as an exclusively Asian epidemic. By the same token, Korea’s success in reducing infections has made it to parts of Western media, but implementation still lags, leading to an explosion of deaths in Italy and perhaps soon France and the US. Hong Kong (from the bottom up) and Taiwan (with government assistance) have limited infection through social distancing and mask wearing, and the West refuses to adopt either.

If it’s Asian, Europeans as well as Americans view it as automatically either inferior or irredeemably foreign. Whatever the reasoning is, it’s an excuse not to learn. Unlike the United States, Europe has pretty good public transportation in the main cities, and a lot of domestic innovations that are genuinely better than what Japan, South Korea, and Taiwan do; thus, it can keep going on like this without visible signs of stagnation. Nonetheless, what Japan has, and to some extent the other rich Asian countries, remains a valuable lesson, which good public transport advocates and managers must learn to adopt to the European case.

Urban rail and regional rail: network design

Tokyo and Seoul both have stronger S-Bahn networks than any European city. This is not just an artifact of size. Paris and London are both pretty big, even if they’re still only about a third as big as Tokyo. In Tokyo, the infrastructure for urban and regional rail is just far better-integrated, and has been almost from the start. Among the 13 Tokyo subway lines, only three run as pure metro lines, separate from all other traffic: Ginza, Marunouchi, Oedo. The other 10 are essentially S-Bahn tunnels providing through-service between different preexisting commuter lines: the Asakusa Line connects the Keisei and Keikyu systems, the Hibiya Line connects the Tobu Skytree Line with Central Tokyo and used to through-run to the Tokyu Toyoko Line, etc.

This paradigm of cross-regional traffic is so strong that on lines that do not have convenient commuter lines to connect to, there are suburban tails built just to extend them farther out. The Tozai Line hooks into a reverse-branch of the Chuo Line to the west, but to the east has little opportunity for through-service, and therefore most trains continue onto an extension called the Toyo Rapid Railway.

On the JR East network, there are a few subway connections to, but for the most part the network has its own lines to Central Tokyo. This is an early invention of mainline rail through-running, alongside the Berlin S-Bahn; the Yamanote ring was completed in 1925. Further investment in through-service since then has given more lines dedicated tracks through Central Tokyo, for capacity more than anything else.

The issue is not just that there are many through-running lines. Tokyo has 15-16 through-running trunks, depending on how one counts, and Paris, a metro area about one third the size, will soon have 4.5. It’s not such a big difference. Rather, Tokyo’s through-running lines function well as a metro within the city in ways the Berlin S-Bahn, the Paris RER, the Madrid Cercanías, and any future London Crossrail lines simply don’t.

What’s more, future investment plans in Europe do not really attempt to turn the commuter rail network into a useful metro within the city. Berlin has a strong potential northwest-southeast S-Bahn route forming a Soviet triangle with the two existing radial trunks, but it’s not being built, despite proposals by online and offline advocates; instead, current S21 plans call for duplicating north-south infrastructure. In Paris, the RER C doesn’t really work well with the other lines, the RER E extension plans are a mess, and most of the region’s effort for suburban rail expansion is spent on greenfield driverless metro and not on anything with connections to legacy mainlines. In London, the subsurface Underground lines are historically a proto-S-Bahn, with some mainline through-service in the 19th century, but they are not really used this way today even though there is a good proposal by railfans.

While Europe generally does the longer-distance version of regional rail better than Japan, the vast majority of ridership is S-Bahn-type, and there, Japan absolutely crushes. What’s more, Korea has learned from Japan’s example, so that the Seoul Subway Line 1 is an S-Bahn and many other lines are very long-range; Seoul’s per capita rail ridership is much lower than Paris’s, but is increasing fast, as South Korea is a newly-industrialized country still building its infrastructure at low cost to converge to Western incomes.

Rolling stock

Tokyo outdoes the closest things to its peers in the West in S-Bahn network design. Japan is equally superior when it comes to the rolling stock technology itself. It has all of the following features:

  • Low cost. Finding information about rolling stock costs in Japan is surprisingly hard, but Wikipedia claims the 10000 Series cost 1.2 billion yen per 10-car, 200-meter train, which is around $60,000/meter, compared with a European range that clusters around $100,000.
  • Low weight – see table here. European trains are heavier, courtesy of different buff strength regulations that are not really needed for safety, as Japanese trains have lower death tolls per p-km than European ones thanks to accident avoidance.
  • All-MU configuration – Japan has a handful of locomotives for passenger service for the few remaining night trains, and runs all other trains with EMUs and sometimes DMUs. Parts of Europe, like Britain, have made this transition as well, but Zurich still runs locomotives on the S-Bahn.

The one gap is that Europe is superior in the long-range regional rail segment with a top speed of 160-200 km/h. But Japanese trains are better at the more urban end up to 100 km/h thanks to their low cost and weight and at the high-speed end of 300+ km/h thanks to low cost and weight (again) and better performance.

Shinkansen equipment is also more technically advanced than European high-speed trains in a number of ways, in addition to its lower mass and cost. The N700-I has a power-to-weight ratio of 26.74 kW/t, whereas European trains are mostly in the low 20s. Japanese train noses are more aerodynamic due to stringent noise regulations and city-center stations, and the trains are also better-pressurized to avoid ear popping in tunnels. As a result, the Shinkansen network builds single-bore double-track tunnels hardly bigger than each individual bore in a twin-bore European rail tunnel, helping reduce cost relative to Japan’s heavily mountainous geography. The EU should permit such trains on its own tracks to improve service quality.

The Shinkansen

The Shinkansen works better than European high-speed rail networks in a few ways, in addition to rolling stock. Some of it is pure geographic luck: Japanese cities mostly lie on a single line, making it easy to have a single trunk serve all of them. However, a few positive decisions improve service beyond what pure geography dictates, and should be studied carefully in Britain, Germany, and Italy.

  • Trains run through city centers with intermediate stops rather than around them. This slightly slows down the trains, because of the stop penalty at a city, and sometimes a slightly slowdown for an express train. This is especially important in Britain, which is proposing an excessively branched system for High Speed 2, severely reducing frequency on key connections like London-Birmingham and London-Manchester.
  • Trains run on dedicated tracks, apart from the Mini-Shinkansen. This was enforced by a different track gauge, but a sufficiently strong national network should run on dedicated tracks even with the same gauge. This is of especial importance in Germany, which should be building out its network to the point of having little to no track-sharing between high-speed and legacy trains, which would enable high-speed trains to run more punctually.
  • Train stations are through-stations (except Tokyo, which is almost set up to allow through-service and errs in not having any). If the legacy station is a terminal, like Aomori, or is too difficult to serve as a through-station, like Osaka, then the train will serve a near-downtown station a few km away, like Shin-Aomori 4 km from Aomori and Shin-Osaka 4 km from Osaka. Germany does this too at Kassel and has long-term plans to convert key intermediate terminals into through-stations, but France and Italy both neglect this option even when it is available, as in Tours and Turin.
  • Rolling stock is designed for high capacity, including fast egress. There is no cafe car – all cars have seats. There are two wide door pairs per car, rather than just one as on the TGV. There is full level boarding with high platforms. Express trains dwell even at major stations for only about a minute, compared with 5 minutes on the TGV and even slower egress at the Paris terminals. Trains turn at the terminals in 12 minutes, reducing operating expenses.
  • Pricing is simple and consistent, without the customer-hostile yield management practices of France, Spain, and much of the rest of Europe.

Reliability

Japan is renowned for its train punctuality. As far as I can tell, this comes from the same place as Switzerland: system design is centered around eliminating bottlenecks. Thus it’s normal in both Japan and Switzerland to leave some key commuter lines single-track if the frequency they run allows timed meets; both countries also employ timed overtakes between local and express trains on double track.

Where I think Japan does better than Switzerland is the use of track segregation to reduce delays. Captive trains are easier to control than highly-branched national rail networks. In Switzerland, there is no room for such captive trains – the entire country has fewer people than Tokyo, and the city of Zurich has fewer people than many individual Tokyo wards. But a big country could in effect turn long lines into mostly separated systems to improve punctuality. This goes against how the S-Bahn concept works in the German-speaking world, but the Tokyo and Seoul lines are in effect metros at a larger scale, even more so than the RER A and B or the Berlin S-Bahn. France, Germany, Spain, Italy, and Britain could all learn from this example.

The heavy emphasis on punctuality in Japanese railroad culture has been blamed for a fatal rail accident. But even with that accident, Japanese rail safety far surpasses Europe’s, approaching 80 billion passenger-km per on-board passenger fatality where Europe appears to be in the low teens.

Is this everything?

Not quite. I will write a companion piece about what Asia can learn from Europe eventually. For one, East Asia appears to optimize its rail operating culture to huge cities, much like France and Britain, and thus its smaller cities have less per capita rail usage than similar-size Central European ones; on this list, compare Fukuoka, Busan, and Sapporo with Stockholm, Prague, Vienna, Munich, Stuttgart, Rome, Frankfurt, Barcelona, and Hamburg. Europe is also better when it comes to 160-200 km/h regional rail.

However, the bulk of intercity rail traffic even in Europe is on high-speed trains, an area in which Europe has more to learn from Japan than vice versa. Similarly, the bulk of individual boardings on trains are on metro and short-range S-Bahn trains even in the German-speaking world; there there is a lot of learning to be done in both directions, but at the end of the day, Tokyo has higher rail usage than Paris and London.

Gap Fillers

The United States is in the process of mandating an innovation commonly seen in Central Europe to guarantee train accessibility: the gap filler, also called the train-mounted extender. When there is a significant gap between the train and the platform, most passengers can still board fairly easily, but passengers who use wheelchairs may get stuck and passengers who have strollers, walkers, or heavy luggage may have difficulties. It is not always possible to reduce the gap to an acceptably narrow level, and therefore some trains have automatic gap fillers mounted on the train extending toward the platform.

What is the gap filler?

Here is a 10-second video of operations in Zurich. The gap filler is mounted on the train and extends over the platform, creating a continuous surface with gentle enough slope that people in wheelchairs can get on unaided. Without gap fillers, sometimes the train-platform gap is too wide and people can get stuck. If the gap gets wide enough, then even able-bodied passengers are at risk of falling through it.

There are also similar operations in Paris and various parts of Germany, though not Berlin. European railroads even use gap fillers when there is no level boarding, to prevent people from falling into the gap between the train and the platform, or to create an external step if the same train serves platforms with different heights one or two steps apart.

Why not just build trains with shorter gaps?

Train widths are not standardized in Europe – the loading gauge in theory permits trains to be 3.15 meter wide, but this is net of curves, so a rigid carbody always has to be somewhat narrower, especially if it is long. That by itself bakes in 10-15 cm gaps.

Two additional effects can create gaps. First, if the train platform is on a curve, then the distance between the most distant point on the train and the platform must increase even if the loading gauge is not defined on a curve. Second, wheels wear out over time, which may create a small vertical gap; if the vertical gap is more than about 2 centimeters then a substantial minority of wheelchair users can’t traverse it (see Barcelona’s universal accessibility plan, PDF-p. 14), and if it is more than 4.5 cm then a majority can’t. Even metro systems, which have level boarding, sometimes have big gaps because of these two effects, requiring manual bridge plates that lengthen station dwells.

Gaps and the United States

The American loading gauge is far more standardized than the European one, since the US is one country and Europe is not. Nonetheless, large gaps exist, for multiple reasons:

  1. The standards for platforms include generous margins: the distance between the track center and a high platform is by law 5′ 7″, and a train is at most 10′ 8″ wide (usually 10′ to 10′ 6″), so the laws already require gaps of at a minimum 3″ (76 mm, about the maximum passengers in wheelchairs can reliably cross) and often 4-7″ (10-18 cm).
  2. The American loading gauge is defined on straight track. Curved platforms require larger horizontal gaps, and as a result many agencies prefer not to build curved platforms at all, even where it is the best design compromise.
  3. There is some amount of oversize freight; the military wishes for a network with generous enough loading gauge to carry tanks.

Gap fillers were unfortunately unknown until recently. MassDOT even used the need for oversize freight as an excuse not to raise the platforms on commuter trains. Instead, American solutions included expensive gauntlet tracks or just keeping platforms low and inaccessible.

Fortunately, once an American implementation of the gap filler existed, namely on Brightline in South Florida, American regulators learned of the existence of this technology, and are now considering mandating it.

Conclusion

There are two conclusions from this story.

The first is that gap fillers are a good technology and more passenger railroads should use them to improve accessibility, not just for passengers in wheelchairs but also ones with strollers or luggage or who are at risk of falling through the gap. The US should aim for universal adoption of this technology nationwide.

The second is that once a good public transportation innovation does reach the United States, it can spread nationally more easily, as globally incurious but nationally curious administrators have a domestic example to look at. This is an example with train-mounted extenders, but the same may be said of fare integration, clockface timetables, lightweight EMUs, and so on. The first agency to adopt any such measure can expect visits from other agencies aiming to learn from its success.

Quick Note: Queer Urbanism

I came out on Twitter the other night. I bring this up here because I was asked something I didn’t, and still don’t, have a really good answer for: how come there are so many queer people, especially ones who are trans or genderqueer, in rail advocacy? This may be just an American question – my impression of German rail advocacy is that it’s much straighter.

On Twitter, there were a few explanations, none of which too satisfying:

  • Autism correlates with queerness (see e.g. here for autism-LGB spectrum correlation and here and here for dysphoria) and also with interest in trains. But then even if one only looks at allistic people, a pretty hefty share of people at (say) TransitMatters are LGBT.
  • Urbanism. The visible queer community is more urban than the general population, for reasons that I don’t want to get into because serious urbanists and Richard Florida have discussed them for decades. Even conditioned on living in a big city with public transportation, the advocacy community is disproportionately queer (again, TransitMatters), but it’s plausible that the same factors making the queer community more urban also make its travel patterns more transit-oriented.
  • Something about American liberal politics mostly drawing from a few groups: queers, Jews, and black people (and maybe other nonwhites). But that is clearly not true of every single political issue, for example the people I can think of in American health care advocacy are straight, and queer activism on health care is often about queer-specific topics like AIDS and trans health care.
  • YIMBY is specifically a fairly queer movement, and the most successful American one, that of San Francisco, is extremely queer; good public transportation advocacy in the US is very YIMBY. But that correlation raises separate questions regarding why good transit advocacy is so YIMBY and why YIMBY has so many LGBT members.

I genuinely don’t know how much of this even holds outside the US. It’s plausible that in countries where passenger rail planning is a career that the average voter of the mainline right party approves of, people with the sexual orientation that the average voter of the mainline right party approves of are more likely to pursue rail advocacy. I don’t have enough knowledge of the political landscape in enough cities to be able to speak comparatively across countries, and if you know more, I urge you to share in comments.

How to Do Coordinated Public Transport Planning

I’d like to share an example of how to implement coordinated planning for public transportation, using an example of something I’ve been working on with TransitMatters in and around Boston. Right now we’re writing schedules and proposing concrete investments including electrification on each commuter line into Boston; the process is different for each line, but the first line we’ve launched the document for, the Worcester Line, is illustrative in itself. You can find the file here and the broader proposal here; the first link bundles two separate documents, of which the Worcester proposal is the second. I’ve harped a lot on using the Swiss model for better regional rail, and here is one example of how to get a city whose rail technology is stuck in the 1930s to have what Zurich has.

Slogans and principles

I’ve harped on a few Swiss and Swiss-adjacent slogans before:

Organization before electronics before concrete. Investments in more tracks, tunnels, and so on should come last as they are expensive, and beforehand agencies should improve signaling and electrify as it is much cheaper. Moreover, fixing organizational issues, for example writing good schedules and integrating planning between different agencies, should come before anything else, as it requires planners to do more work but is otherwise cost-free.

Takt and symmetry. If a train leaves your station going eastbound at 7:14 am and the schedule is every half hour, then a train leaves your station going eastbound at :14 and :44 all day, every day; this is also called a clockface schedule. If there’s additional service during rush hour, it should fit into the takt, e.g. more trains coming at :29 and :59 for 2 morning hours and 2 afternoon hours. By the same token, trains going westbound should serve your station at :16 and :46, since 60-14 = 46. This means the overtakes, meets on a single-track line, etc. all occur at consistent places.

The magic triangle of infrastructure, rolling stock, and timetable. The plan must account for all three sides of the triangle simultaneously, in order to optimize investment. For example, if additional tracks are required for timed overtakes, then the agency should know what trains it’s going to run and how frequent it’s going to run them in order to know where the overtakes are needed. With a takt, the overtakes will be at consistent location where the region can target investment.

Run trains as fast as necessary. Increases in speed should be designed around making timed connections and limiting train downtime. One refinement on a suburban line is that the stop spacing should depend on the schedule: if the one-way trip time is 52 minutes then a short turnaround makes an hour and additional stops are difficult to fit in, whereas if it is 46 minutes then the turnaround is longer and there is room for more stops.

The knot system: knots (or nodes, same word in German) occur at major stations at regular intervals – at a minimum an interval equal to half the systemwide takt frequency. If trains run half-hourly, then a station with service at :00 and :30 or with service at :15 and :45 will be served in both directions at the same time, so it’s a good place for bus and train connections. This works in both planning directions: if the schedule happens to place a knot at a station then buses should go there, and conversely if a city is a major node then the schedule should be written to a place a knot there.

What we propose for Worcester

The proposal as written calls for two service patterns, one express and one local. At rush hour, both run every 15 minutes. Off-peak, the express pattern drops to 30-minute frequency, but the local pattern stays at 15 minutes, as it serves Boston neighborhoods and Newton, close enough in that high off-peak ridership can be expected. With electrification and high platforms, the following schedule is feasible:

Station Km-point Local Express
Boston South 0 0:04 0:11
Back Bay 2.1 0:07 0:14
Lansdowne (Fenway Park) 4 0:09 0:16
West (Allston) 6.2 0:12
Boston Landing 7.5 0:14
Newton Corner 11.3 0:17 0:21
Newtonville 13.3 0:19
West Newton 15.2 0:21
Auburndale 16.9 0:23
Wellesley Farms 20.3 0:26
Wellesley Hills 21.8 0:28
Wellesley Square 23.8 0:30
Natick 28.5 0:34
West Natick 32.1 0:36
Framingham 34.3 0:39 0:32
Ashland 40.5 0:36
Southborough 44.2 0:40
Westborough Center 51.5 0:44
Grafton 58.7 0:49
Worcester 71.3 0:56

Express trains overtake locals at Wellesley Farms; there are plans for triple-tracking Wellesley (and farther west, but it’s not necessary). At Framingham, locals take 12 minutes to turn, which means there needs to be a non-revenue move around 0:41 westbound to a yard just west of Framingham to avoid getting in the way of express trains at :43 and :47 before getting back to Framingham at 0:49 to collect passengers; triple-tracking Framingham is also an option but is more expensive.

How it fits the principles

Let’s go over the Swiss principles one by one and see how this all fits.

Organization before electronics before concrete. As presented the plan includes elements of all three: organization is better-timed schedules and the potential use of the yard as a pocket track to avoid triple-tracking Framingham, electronics is electrification, concrete is the triple track. The electronics-concrete order is important – without the triple track but with electrification, EMUs can still do Boston-Worcester in around 57 minutes with the above stops, or 55 without infill at West Station and Newton Corner, either of which is faster than the fastest express trains today. The ultimate in concrete in the Boston area is the North-South Rail Link, which should come only after full electrification and related modernization steps, such as high platforms.

Takt and symmetry. The timetable is on a takt and symmetric, to ensure the overtake takes place at a manageable spot in Wellesley. It would be easier to change the offset slightly and overtake around West Newton, but there the tracks are in a constrained location where triple-tracking is prohibitively expensive. Note also that with the above timetable, the westbound overtake is at :11, :26, :41, :56, and the eastbound overtake is at :04, :19, :34, :49, which means it requires triple-tracking but not four-tracking.

The magic triangle of infrastructure, rolling stock, and timetable. The timetable is calibrated around the performance specs of the latest EMUs, like Coradias, Mireos, Talent 3s, and FLIRTs. The high acceleration capabilities of these trains let a local train leave Boston just 7 minutes ahead of the next express train, and still keep up through double-track narrows in Newton until Wellesley Farms, the sixth station skipped.

Run trains as fast as necessary. Without onward connections beyond Worcester, transfers between trains are not really a factor. Thus, what matters is tight turnaround times to keep trains moving and earning revenue rather than loitering at the terminal. The local train spends 35 out of 45 minutes running, and the express train 45 out of 60.

The knot system. Knots occur wherever trains stop around :00, :15, :30, and :45. The word around includes a few minutes of wiggle time, especially at a terminal, where transfers are unidirectional. Thus Worcester is a knot at :00, with a few minutes of rail-to-bus and bus-to-rail transfer. Framingham is a knot at :30, as long as the buses get there before :28 to transfer to eastbound express trains and depart after :32 to accommodate transfers from westbound express trains. On local trains, Newton Corner may be a knot, with a connecting bus shuttle to Watertown.

Bus nodes

Framingham and Worcester already exist as bus nodes, and in both cities, the main city bus hub is already the train station. The next step is to integrate the schedules. The rule is generally that bus timetabling should follow rail timetabling, because trains require more infrastructure whereas buses can be moved more easily; there are exceptions, but not many.

The principles for bus design on the Zurich model aren’t as catchy as for rail design, but they are still useful and generally worth learning:

One ticket for all. Fares must be totally integrated. If a train makes two stops in the same zone (for example, Framingham and West Natick), it should charge the same as a bus. A train ticket should be valid within the entire zone traversed, which includes bus transfers. The same fare media should be used on all modes – and they should be paper tickets with no surveillance, not Boston’s ongoing smartcard disaster (“AFC 2.0”). Fare integration requires a mechanism for sharing revenue across agencies, but this is organization, and is doable under the aegis of the Massachusetts state government, with revenue allocated to agencies based on periodic counts to ascertain ridership (Berlin’s are every 3 years).

Timed transfers. Suburban buses should come every half hour, on a takt of course, with timed transfers to the trains at the relevant knot. Worcester’s bus agency, WRTA, does not do this at all – bus #1 runs on an hourly takt, but other routes may run every 50 minutes or every 75. Framingham’s, MWRTA, has 65-minute headways, and a route that runs to a Green Line station rather than much closer to a commuter rail station.

High vehicle utilization. If the bus takes around 25 minutes to reach its outlying destination, then two vehicles serve one route, and if it takes 40 minutes, then three vehicles do. Buses should run as fast as necessary as well, deleting meanders, installing queue jump lanes, and shortening the route in order to squeeze inside a timetable with short turnaround times.

Connections between different train stations. A bus can connect two different train stations, either on the same line or on different lines. It should be timed at both ends, though it if runs parallel to the train, then it’s fine to time only right-way connections (e.g. eastbound bus to eastbound train, westbound bus to westbound train), which do not require knots.

Our Project

Eric Goldwyn and I have just signed a two-year grant contract for our big construction cost project; we’re working via NYU, him on-site in New York and me remotely in Berlin (at least for now).

We’re hiring!

Our budget includes extensive spending on people who are not Eric or me. For now, we are looking for part-time grad student work to help with data collection. We have an ad circulating internally around NYU, but it’s also open to outsiders:

We are looking to hire up to three students from around the university to help us compile data on infrastructure costs from around the world, especially those of urban subway lines. Specifically, we are looking to understand the drivers of costs—why do public transportation infrastructure projects in one city cost more than in another city? We have already begun collecting this data on projects from around the world and would like to extend these efforts.

We are particularly looking to extend our coverage outside countries where information is readily available in English, such as the English-speaking world or Western Europe. The information we need consists first of all of headline costs of public transportation infrastructure costs, but then of more detailed breakdowns, such as construction techniques, ancillary projects, financing mechanism, the environmental review process, the legal situation, labor size, etc.

The ideal candidate will thus have the following skills:

  • Reading fluency in a foreign language used in a country or countries with major ongoing urban rail construction, such as Chinese, Korean, Spanish, Russian, or Arabic.
  • Either preexisting familiarity with engineering terms (such as “cut-and-cover”) or the ability to learn them quickly.
  • Database software, such as Excel or more advanced statistical analysis software.
  • Data analysis or data science techniques useful for small N.
  • Self-motivation and independence, for example in finding relevant information to add to the database.
  • Good oral and written communication skills.
  • Punctuality and promptness – deadlines are written in stone.

Drs. Alon Levy and Eric Goldwyn will supervise all students and work side by side with them to extract the most value from the data. There will also be opportunities to collaborate on writing projects related to the data collection efforts.

If you’re interested, please email both me at alon@pedestrianobservations.com and Eric at elg229@nyu.edu. If you only have half the listed skills, you should probably still apply, especially if these skills include a foreign language that other applicants won’t know.

We will also hire more people as time goes by. We have a budget for a postdoc-level research scholar, so if you’re graduating this year please keep in touch – I’ll post updates when we know our exact timeline, since the grant period isn’t neatly in line with academic years, but it’s a minimum one-year full-time position at NYU, one that for visa purposes is treated as an academic job (thus exempt from the work visa cap).

The goal

The ultimate deliverable in the project is a long report – I’m guessing mid-3 figures number of pages – detailing why American costs are high and what can be done about it. The report should include the following:

  • The database of construction costs, broken down to include not just headline costs but also details about construction methods, construction costs by component (stations, tunnels, systems, etc.), rock type, procurement methods, and other relevant variables.
  • A highlight of what the important variables are for explaining differences in construction costs, including hopefully a few sentences about the situation in each major city in the database (or if not each then many, on the order of 30+).
  • Potentially related databases of construction costs if we get them in sufficient detail and judge them to be comparable, such as for road tunnels, high-speed rail, rail electrification, surface tramways, and urban rail accessibility retrofits.
  • A brief how-we-got-here historical overview covering institutional and engineering background to how American infrastructure construction differs from that of most other countries.
  • Six (at least) detailed city-level case studies. New York may or may not end up as one of them; Boston almost certainly will, for work we have been doing about the Green Line Extension. The case study selection needs to happen early – this calendar year, and not near its end – and this means we need to identify solid sources who will speak to us about the historical, institutional, legal, and social factors at play.
  • A conclusion synthesizing everything to give a coherent recipe for how American (and really English-speaking in general) cities can reduce their construction costs to rest-of-world levels, and ideally even further to match the costs in cheaper countries like Spain, Switzerland, Italy, South Korea, Romania, and the Nordic countries.
  • A higher level of synthesis suggesting what a rail network for New York could look like at the lower costs we are proposing.

If you know sources who can talk to us – for example, people at agencies that are building urban rail outside the English-speaking world – then please reach out to us.

The test

I feel good about this – about the recognition, and about the ability to study comparative costs without the stress of looking for temporary gigs. I’m reaching out to various contacts and contacts-of-contacts in a number of cities that are building urban subways, and if anyone has suggestions for who I should talk to, please shoot me an email or mention what you know in comments, as this is a field with a huge base of knowledge.

But at the same time I feel terrified, because I can fail. The project is not going to completely flop, because the database already exists and there’s even more data out there that we already got but just haven’t published. But from getting even an exhaustive database to being able to make actionable recommendations the route is long, and involves case studies and qualitative research and emailing people who have no reason to have heard of me or Eric and often just don’t respond. I think it’s very likely we’ll be able to come up with a useful writeup, and decently likely that this writeup will include a recipe for building subways in New York for $200-300 million per kilometer rather than $2 billion ($100 million/km, as in Madrid and such, is aspirational).

But it’s not guaranteed. We can fail at any number of places: managing the students, finding detailed enough cost breakdowns to identify where the US fails, having broad enough coverage to write multiple case studies, getting enough experts who’ve built cheap subways to talk to us, and so on. The report I mentioned above will get written and published, but whether there is an actionable conclusion remains to be seen, and even if the conclusion is actionable, I don’t know how politically realistic it will be.

Doing this research without really knowing what we’ll find is frustrating this way. The conclusion may well be “the US needs to bust the construction unions.” I don’t think such a conclusion is likely from what we’ve seen so far, but I cannot 100% rule out that it is a significant factor. Or it may be “the US needs to get rid of common law,” which is even less likely to happen; I thought this was an important factor until 2018 or 2019. What is likelier is that a lot of local notables and small-time bureaucrats may need to be cut out of the loop entirely through more streamlined project reviews with fewer veto points, which is politically plausible but requires a governor or a federal government with a modicum of political courage to execute.

What it means for this blog

I’m going to keep posting, at the usual rate of twice a week averaged over time. If I find interesting snippets, I may post them before releasing the report; to some extent I’ve already been doing that with smaller projects. I am still going to think a lot about issues of network design and urbanist politics and will keep writing about those topics.

My Patreon is still around if people want to give me money even though I’m not lacking for it at this point. I’ve been slouching on some of the rewards as I spent months not freelancing (thus, not getting ideas to mine for extra backers-only posts and polls) but finalizing this contract, and now that I have the contract at hand and the project is starting I can go back to it as promised.

In parallel with the costs project, I am going to keep thinking about network design and come up with proposals like this one for New York and New England or this one for Germany; I’ve been thinking about an integrated America-takt or a Europe-takt, at vastly larger scale than any national plan so far, even China’s (which only covers high-speed rail and has no regional rail worth mentioning). Subject to upcoming election results, the scope of what budget is realistic may be narrow enough that I can think in terms of what a specific dollar or euro figure could do.

This of course relates to construction costs – the lower the costs, the more stuff can be built for the same amount of money. Moreover, at high enough level, absolute costs do matter: a Green Deal with €150 billion investment Germany-wide or a Green New Deal with $600 billion US-wide is a big enough proportion of GDP so as to hit real limits to tax capacity and deficit spending, so reductions in unit costs are in 1-to-1 correspondence with building more green infrastructure.

This is why costs ultimately matter. A single subway project may look like a drop in the bucket of the national budget, but when it’s bundled with the costs of an entire public transportation network, and those costs in turn are bundled with those of other major government priorities, the drop becomes a bucket and then a river and then an ocean. The biggest successes in public transportation are plans that look at everything simultaneously and integrate every aspect of operations and infrastructure, and the more cost-efficient these plans are, the further they can reach. There is no way around it.

MAGA Trains

American railfans are full of nostalgia for a past era when American trains were great. So much of the discussion among industry insiders, railfans, and advocates is about how to make American railroads great again, how to return to the mid-20th century era of American domination. This is not correct history: while American railroads were in fact in a pretty good position from the 1920s to the 50s, they were not competitive with mass motorization and air travel, and trying to imitate what they were like then has no chance of competing with cars or planes. The story of American railroads has to be understood not as decline but as stagnation: operations, technology, and management stagnated, and this is what led to ridership decline. Instead of indulging in a MAGA fantasy about past greatness, it is important for the United States to implement all the innovations of the last half century that it has missed out on, innovations coming from East Asia and Western Europe.

Organization

American railroads were private until Amtrak took over intercity operations and states took over commuter rail operations, which happened well after the terminal decline in ridership. There was intense competition between rival companies, at times leading to physical violence. There was no coordination of operations between different railroads, no coordination with municipal public transportation systems, no attempt at seamless passenger experience. What was the point? This system evolved in the early 20th century, when there was no competition from other modes, only from other railroads.

Over time, most of the rest of the developed world has learned to coordinate different modes of public transportation better, to compete with cars. This usually occurred under nationalized mainline rail companies, but even when companies remained separate, as with the division between municipal subways (e.g. the Berlin U-Bahn) and national railways (e.g. the S-Bahn), or with the separate BLS system around and south of Bern, there has been integration. There is fare and schedule coordination in German cities across rail and bus operators, and even better coordination in the Netherlands and Switzerland.

The US remains fixated on competition, and thus there is no fare integration, but rather relationships between different operators are adversarial. In Chicago, the mayor opposes integration between the municipal L and the regionally-owned Metra commuter rail system, since the city does not own Metra. Every time Amtrak has to share territory with a commuter railroad, one side is screwing the other out of something, whether it’s Amtrak overcharging on electricity or Metro-North arbitrarily slowing Amtrak down. In Boston, there is no integration between city-focused MBTA service, which includes commuter rail, and buses in outlying cities, called RTAs (regional transit authorities); the MBTA is simply uninterested in matching fares or schedules, and is not even integrating its own buses with its commuter trains.

Planning coordination

Switzerland has higher rail usage than every place I know of once one controls for city size. Zurich’s modal split may not be as favorable to public transportation as Paris or London’s, but is a world better than that of any French or British city of similar size. Switzerland got to this point through a stingy political process in which planners had to stretch every franc, substituting organizational capacity for money. Thus, construction in the 1990s used the following principles of value engineering:

  • Infrastructure, rolling stock, and the timetable should be planned together (the magic triangle), since decisions on each affect the other two.
  • Trains should run as fast as necessary for transfer windows, overtakes, meets on single track, etc. Infrastructure should likewise be only as expansive as necessary – if the timetable does not have trains on a given single track meeting, this segment does not need to be doubled.
  • Trains should have timed transfers at major cities, to enable everywhere-to-everywhere travel. Connecting buses should be timed with the regional trains at major suburban nodes.
  • Electronics before concrete: it’s cheaper to resignal a line to have short headways and high speeds than to add tracks and tunnels.

These principles do not exist in the United States. Worse, too many American activists, even ones who are pretty good on related issues, do not believe it’s even possible to implement them. “This isn’t Switzerland or Japan” is a common refrain. There’s growing understanding among American cycling advocates that 50 years ago the Netherlands wasn’t as bike-friendly as it is today; there sadly isn’t such understanding regarding the state of rail coordination in Switzerland until about the 1990s.

While Switzerland manages to build its Knot System at low cost, leading to sharp increases in rail usage in the 2000s and 2010s, Americans are unable to do the same. Activists propose massive spending, which the political system is unwilling to fund. Nor is the political system interested in adapting low-cost solutions for infrastructure coordination, since the sort of apparatchiks who governors like appointing to head state agencies can’t implement them; we all know what happened last time a foreigner got appointed to a major position and succeeded too much. The way forward is right there, and the entire American political system, from every governor down to most activists, either is ignorant of it or explicitly rejects it.

Technology

Amtrak runs slower than it used to on most lines. Trip times on the Northeast Corridor south of New York are if anything slightly slower than they were in the 1970s in the early days of the Metroliner. The corridor and long-distance service outside the Northeast are considerably slower. For example, the Super Chief took 39:45 between Chicago and Los Angeles, whereas its current Amtrak version, the Southwest Chief, takes 43:10. At shorter range, the Chicago-St. Louis trains take 5:20 today, compared with 4:55 in the 1930s. This has led too many Americans to assume that there has been technological regression and that the main focus should be on restoring midcentury service levels rather than on moving forward.

In reality, high speeds in the middle of the 20th century came from the facts that express passenger trains were highly profitable and used by important people and so had priority over all other traffic, and that superelevation was set high for these trains; both of these aspects collapsed as riders and high-value shippers decided driving and flying were better than taking 5-hour train rides, so the profit center shifted to low-value freight. Today, getting high passenger ridership is plausible at high-speed rail speeds, but that requires getting Chicago-St. Louis down to 2 hours, not 5 hours, and having excellent connections to local and regional public transportation at both ends.

Nor was midcentury rolling stock good by current standards. Electric locomotives in Europe weigh around 90 tons. American ones weigh a little more, still in compliance with superseded FRA regulations enacted just after WW2. But the locomotives from just before these regulations weighed far more: the Pennsylvania Railroad’s GG1 weighed 215 metric tons. Europe has achieved weight reductions over generations of innovation since, and Japan has achieved even more impressive reductions; 215 tons would get you 2/3 of the way to a 10-car EMU set in Tokyo.

Worse, even in the middle of the 20th century, the US was no longer at the technological forefront of rail service. The civil service formation following the German Revolution brought forth a new railway law and new technology, such as the tangential switch, since adopted throughout Continental Europe; the US mostly sticks with secant switches built to late-19th century specs. In the 1950s the differences between German and American rail technology weren’t huge, but they were there. Since then they’ve gradually widened – in the 1960s Germany came up with LZB signaling, while the US was at best stuck on 1930s signaling, federal regulations on the matter leading to lower top speeds than to the adoption of automatic train protection.

There seems to be general ignorance of the advances that the US has not been part of. Rail managers ask questions like “does Europe have positive train control?” (yes, ETCS is already a second-generation system, we just call this automatic train protection instead of positive train control) or say “Europe doesn’t have the ADA” (accessibility laws here are comparable to American ones and overall the public transportation networks here are on average more accessible). In technology as in organization, the MAGA mentality for trains refuses to admit that there are innovations abroad to learn from.

The way forward: imitate, don’t innovate

The United States can innovate in public transportation, but only if it imitates better countries first. It needs to learn what works in Japan, France, Germany, Switzerland, Sweden, the Netherlands, Denmark, South Korea, Spain, Italy, Singapore, Belgium, Norway, Taiwan, Finland, Austria. It needs to learn how to plan around cooperation between different agencies and operators, how to integrate infrastructure and technology, how to use 21st-century engineering.

There are great places where such imitation could work. I work a lot on Boston-related issues at TransitMatters; New England has high population density, a wealthy and growing urban core in Boston, ample legacy rail infrastructure, and town centers that work more like Central European suburban sprawl (albeit at lower density) than like structureless Californian or Texan sprawl. But it can’t move forward without rejecting MAGA fantasies and replacing them with a program of learning from what works here and in Japan. There are so many projects under discussion of limited or no value, and some even with negative value, like anything that interacts with the hobby freight railroad Pan Am.

Instead, the tendency in the United States is to do anything to avoid learning from outside North America. Plans for intercity rail improvement outside the Northeast and California are steeped with MAGA language about restoring midcentury rail. Plans in New York spend far too much time on midcentury expansion plans and far too little on understanding cost explosion factors dating to the 1920s. Regional rail plans vaguely nod to European S-Bahns, but are generally filtered through several layers, mainly Philadelphia’s implementation. Anything that touches freight invites kludges that European planners no longer use for cost or maintenance reasons.

This tendency has to end. Meiji Japan didn’t join the first world by closing itself to foreign inventions – quite the opposite. The US needs to understand that the path to a future with better American transportation lies not in America’s past, but in Europe and East Asia’s present. The history isn’t one of American decline and renaissance through rediscovery of ancient learning, but one of American insularity and stagnation, to which the solution is to adapt technologies that work elsewhere.

Freight Rapid Transit

Is it possible to use a rapid transit-style system to carry light freight, such as parcels? So far no such system exists, and very few semi-relates systems exist (like pneumatic tubes for mail). But it remains an interesting potential technology, provided it is done right. Unfortunately, it is very easy to do it wrong through misunderstanding how freight or how rapid transit works. Therefore, advances in policy in this direction are good but should be done carefully.

Instead of giving people one big takeaway, I’m going to suggest a few good principles for this, motivated by both good and bad proposals.

1. Keep the tracks clear for maintenance at night

Germany’s minister of transport, CSU’s Andreas Scheuer, proposed running freight on the U-Bahn after hours. This is a terrible idea: regular nighttime closures are crucial for maintenance, and without them, maintenance costs go up and daytime reliability tanks. New York’s constant weekend service changes are the result of not shutting down overnight for maintenance nor being able to reliably single-track at nighttime headways. Berlin already runs overnight on weekends and does some daytime maintenance – “Ersatzverkehr mit Bussen” is one of the first ordinary German phrases I learned after moving here. Further encroachment on maintenance windows is not acceptable.

2. Use existing station infrastructure

The main cost in digging urban rail tunnels is the stations – boring tunnels between stations is a solved problem. This means that the main difficulty of urban rail freight is where freight gets on and off the trains. Loading and unloading container-size freight is impossible without massive station digs, all in expensive places. Having a freight car wait on a siding is not possible either – that interface between the customer and the freight railway relies on cheap land and time-insensitive shipping.

Most likely, shipping parcels by rapid transit requires using the existing stations and platforms. There is almost certainly no room at rush hour, when trains are sized to take up the entire platform interface to increase capacity. But in the daytime off-peak, there may be some room for using a portion of a subway station for parcels.

3. Keep up with passenger rail traffic

If freight trains can’t run at night, they have to slot on the same timetable as passenger trains. This isn’t a problem on the tracks – just add an EMU car loaded with parcels rather than passengers. But keeping dwell times under control is critical. Alert reader Mordy K. wrote about this, suggesting a “dynamic Rubik’s cube” that “shifts the packages around in 3D.” This is the real challenge: figure out how parcels get from the train to a designated spot on the platform or from the platform to a designated spot on the train during a 30-second dwell time.

4. Be aware of all interfaces between different systems

There are, at a minimum, five legs to a parcel trip in a city using rapid transit: origin to station, station to train, trip on train, train to station, station to destination. The boarding and alighting steps, so easy for the able-bodied passenger and even for the disabled passenger given rudimentary investment into accessibility, are difficult for a parcel of freight. Tossing a package from a train to the platform is not enough: the package needs to get to the surface for the final leg of the trip. A courier could carry it, but at a high cost – the courier’s modes of transportation for the surface legs, like the e-bike, are bad at getting down to the subway and back up, so the time and physical effort costs are high.

This in turn means that the rail transit freight system needs to be able to put parcels in a freight elevator. Elevators are not free, although they are rarely as expensive as in New York. The problem is that parcels can’t walk across the platform, so the elevator has to face the exact same place every time, which may run into construction difficulties.

5. Don’t wreck passenger rail service

Berlin runs some trains short, especially after hours. Usually the first train after the beginning of short train service is very crowded, because passenger service demand is still too high for a half-train at the typical density of daytime Berlin trains. (I say typical density because I have never seen a Berlin train as crowded as the busiest off-peak trains in Paris or New York, let alone their busiest peak trains.)

What this means is that in practice there isn’t that much space on the train for freight. Running trains every 5 minutes until later at night but then cordoning off half for freight may be feasible – right now headways rise to 10 minutes around 9 in the evening – but it’s still just a few evening and early night hours for delivery.

This principle is equally important at the stations: cordoning off parts of the platform for freight is fine, but only if it does not interfere with passenger capacity or circulation. This may further constrain where freight elevators go: whatever automated system gets parcels from the train to the elevator will have to cross passenger traffic at-grade, and driverless technology can do it but not cheaply or smoothly.

6. Aim to work with a wide range of goods

Pneumatic tube systems for mail work for mail, but modifying them for other goods isn’t trivial. In contrast, a parcel delivery system should aim to be broadly usable by many goods with a high ratio of value added to weight. Subtle differences are important at this level of detail: glass and china goods can’t be thrown on the floor, fresh food spoils if it’s left outside for too long, jewelry and electronics face a high risk of theft. The technology has to have adequate tracking, punctuality, defense from shocks, and so on.

7. Be aware of the competition

Delivery by rapid transit is not the only alternative to trucks for cross-city shipping. Delivery by drone is in active development, both surface drones and flying drones. Surface drones have good synergy with trains, since surface drones are slow and make better first- and last-mile connections. But flying drones are in direct competition, since they work well at a range of a few kilometers rather than a few hundreds of meters. Flying drones so far only work at extremely high value-to-weight ratios, but if they become more widespread, it’s useful to think of how urban rail can compete.

China Won’t Save You

The construction costs of Britain’s just-approved domestic high-speed rail network, High Speed 2, are extreme. The headline costs are, in 2019 figures, £80.7-88.7 billion per the Oakervee review, with one estimate going up to £106.6 billion, all for a system only 530 km in length in mostly flat terrain. This includes rolling stock, but that is less than 10% of the projected cost. At the end of the day, Britain has decided to spend around $200 million per kilometer, a cost comparable to that of base tunnels and mostly-tunneled high-speed lines.

And now the People’s Republic of China has offered to build the entire thing for cheaper with a 5-year timeline, and everyone acts as if it’s a serious offer. So let me dust off my construction costs database and tell you: the PRC won’t save you. There is no alternative to developing good internal cost control. This requires learning from lower-cost countries, but Chinese high-speed rail construction costs are not really low.

Vietnam

Ho Chi Minh City and Hanoi are both building metros. Hanoi uses Chinese financing, HCMC uses Japanese financing. Both have very high construction costs – my database has HCMC’s 13% underground Line 1 at $320 million/km, 82% underground Line 2 phase 1 at $535 million/km, and 84% underground Line 5 phase 1 at $590 million/km, whereas Hanoi’s 74% underground Line 2A is $215 million/km and 32% underground Line 3 is $365 million/km.

The system in Hanoi has been plagued with delays. Line 2A was supposed to be operational by 2016. Construction was only completed in 2018, but the line is yet to open. Testing is ongoing, but Chinese experts couldn’t return to Vietnam after the Chinese New Year holiday because of the coronavirus quarantine. The South China Morning Post has compared the Hanoi project negatively with that of HCMC, which is for the most part on time, if expensive.

Like many developing-world cities, HCMC is paying more for a subway tunnel than Japan pays at home; to get to the cost range of HCMC in Japan, one needs to go to complex regional rail tunnels in Tokyo dipping under multiple older tunnels in city center. In that it is no different from Dhaka or Jakarta. The primary explanation must be that importing Japanese technology means using techniques optimized for a high-skill, high-wage labor force and cheap domestic capital, rather than ones optimized for a low-skill, low-wage labor force and expensive imported capital.

But that does not explain why the Hanoi Metro is so expensive. Chinese metros cost less (though not universally – Shanghai’s construction costs are rising fast): I want to say about $250 million/km on average, about the same as the non-Chinese global median, but the actually big set of data is unpublished so you guys can’t nitpick my sources yet. So what’s going on here? Vietnam is poorer than China, but the difference is not so big. It’s about half as rich as the PRC. It’s comparable to Europe, where Romania and Bulgaria are about half as rich as Western Europe, and they have low construction costs, lower than parts of Eastern Europe closer to Western incomes.

Chinese high-speed rail

The construction costs of high-speed rail in the PRC are fairly high, especially in its richer parts. The costs remain lower than those of tunnel-heavy lines like those of Italy, Japan, and South Korea, but by low-tunnel standards, they are high.

There is a perception that Chinese costs are low, but it comes from using the wrong currency conversion. Here, for example, is a World Bank report on the subject:

[P. 39] Figure 4.1 shows the construction cost of 60 projects. The average cost of a double-track HSR line (including signaling, electrification, and facilities) is about Y 139 million/km (US$20.6 million/km) for a 350 kph HSR line, about Y 114 million (US$16.9 million) for a 250 kph HSR line, and about Y 104 million (US$15.4 million) for a 200 kph HSR line. These costs are at least 40 percent cheaper than construction costs in Europe (European Court of Auditors 2018, 35).

The problem is, the exchange rate of $1 = ¥6.75 is incorrect. The OECD’s PPP conversion factor today is much higher, $1 = ¥3.5; for high-speed lines built a decade ago, it would be even higher, about $1 = ¥3.3, with ten years of American inflation since. Using the correct modern rate, the cost is about $40 million per kilometer, which is not lower than in Europe but rather higher. Beijing-Shanghai, as far as I can tell a ¥220 billion project for 1,318 km of which just 16 km are in tunnel, rises to $50 million per km, and more like $60 million per km in today’s money. It’s still cheaper than High Speed 2, but more expensive than every Continental Europe high-speed line that isn’t predominantly in tunnel, like Bologna-Florence.

There are all these longwinded explanations for why the PRC does things cheaper and faster than the first world, and they are completely false. China is not cheap to build in, especially not high-speed rail. The only reason Chinese costs aren’t even higher is that Eastern China is pretty flat. Even then, China has not taken advantage of this flatness to build tracks at-grade to minimize costs. Instead, it has built long viaducts at high cost, in contrast with the at-grade approach that has kept French LGV costs reasonable.

The PRC doesn’t even build things particularly quickly. Total actual construction time from start to finish per line segment is 4-6 years per Wikipedia’s list, which is comparable to recent LGVs. What is true is that China has been building many lines at once, and each line is long, but this is a matter of throughput, not latency. The limit to throughput is money; the PRC made a political decision to spend a lot of it at once as stimulus in the late 2000s and early 2010s, and by the same token, the UK has just made a political decision to spend just less than £100 billion on High Speed 2, in a trickle so that the system will take 15+ years to complete.

Why are they like this?

The myth of hyper-efficient Chinese construction seems never to die; I’ve seen it from the first days of this blog, e.g. then-US Secretary of Transportation Ray LaHood in 2012. It relates to a mythology that I think is mostly part of Anglo-American culture, of the tension between freedom and efficiency. The English-speaking world in this mythology is the epitome of freedom, with a gradation of less free, more efficient paces: Germany, then Japan, then finally China. It’s a world in which people’s ideas of what totalitarianism looks like come from reading George Orwell and not from hearing about the real-life Soviet Union’s comic incompetence – the gerontocracy, the court politics, the drunk officials, the technologically reactionary party apparatchiks – all of which was happening in real time in Nazi Germany too, which was fighting less efficiently than the UK and US did.

It’s equally a world in which people think rights Germans and Japanese take for granted, like various privacy protections, do not even register as important civil liberties. I dare any reader to try explaining to a British or American transit manager that really, no, you do not need our data, Central Europe manages to plan better than you without smartcards tracking users’ every move and storing the data in servers with infosec that screams “steal me.” Nor do Americans make much of an effort to import policing regimes from democracies with one twentieth their rate of police shootings per capita.

China’s incompetence is now visible to the entire world, in the form of a virus outbreak that local officials flailed about for a month, too afraid to acknowledge mistakes lest they take the fall for them. And yet it’s easier for American and British business leaders and politicians to point to China as an example to emulate than to Pareto-better France or Germany.

If anything, High Speed 2 is low-key overlearning some French lessons, leading to inferior infrastructure planning – but it’s messing up key details leading to cost explosion, such as “don’t build new signature urban train stations.” But my suspicion is that French and German rail experts will point out all those details. To us, if Britain changes some detail in a way that isn’t truly justified by local conditions, we will point it out – and push back when British blowhards try to explain to use that they do things differently because they’re morally superior to us. British people know this – they know they can’t pull rank. Americans are the same, except even less capable of dealing with other nations as equals than the British are.

The way forward

High Speed 2 is a mess, largely because of the cost. To move forward, talking to China about how it’s built high-speed rail may be useful, but it can’t be the primary comparison, not when Continental Europe is right here and does things better and cheaper. For Asian help, Japan has some important lessons about good operations and squeezing maximum use out of limited urban space. A lot of scope can be removed. A lot more can be modified slightly to connect to regional lines better.

More conceptually, Britain has a problem with costs and benefits chasing each other. If benefits are too high, the political system responds with sloppy cost control, for example by lading the project with ancillary side projects that someone wants or by giving in to NIMBY opposition. If the costs are too high, the political system responds with scrounging extra benefits, for example counting the consumer surplus of high-speed rail travelers as a benefit, by which standard every government subsidy to anyone has a benefit-cost ratio of at least 1.

Bringing in the PRC won’t help. It’s value-engineering theater, rather than the hard work required to coordinate infrastructure and timetable planning or to tell Home Counties NIMBYs that the state is not in the business of guaranteeing their views; there is so much tunneling on the proposed line that isn’t really necessary. None of the countries that builds trains cheaply did so by selling its civil service for spare parts; why would Britain be any different?

Metcalfe’s Law for High-Speed Rail

I wrote a Twitter thread about high-speed rail in the United States that I’d like to expand to a full post, because it illustrates a key network design principle. It comes from Metcalfe’s law: the value of a network is proportional to the square of the number of nodes. The upshot is that once you start a high-speed rail network, the benefits to extending it in every direction are large even if the subsequent cities connected are not nearly so large as on the initial segment. Conversely, isolated networks from the initial segments are of lower value.

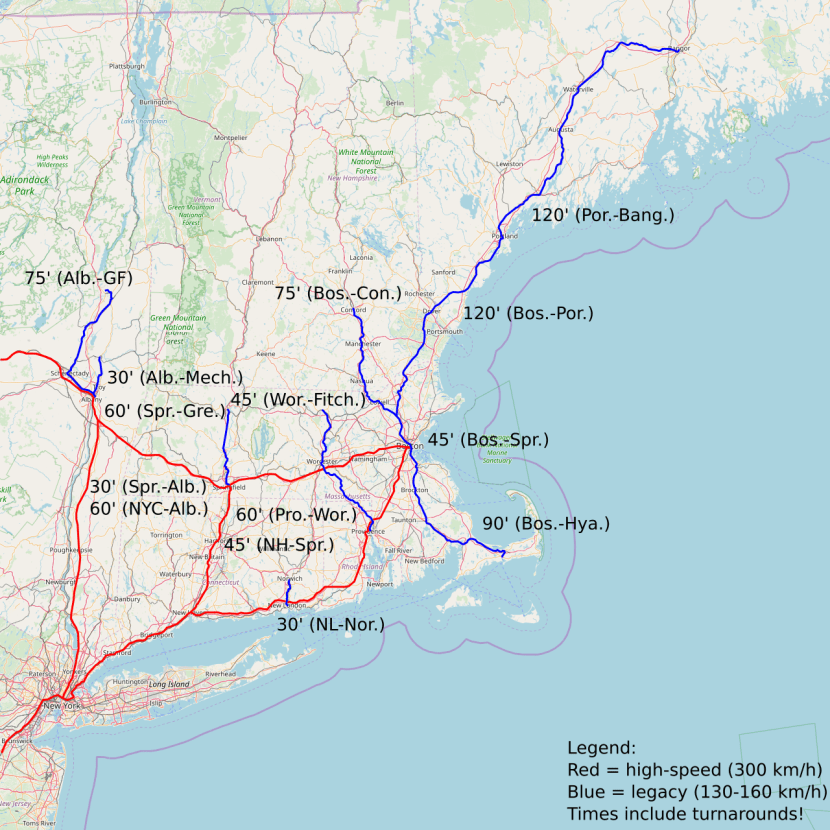
The implication for the United States is that, first of all, it should invest in high-speed rail on the entire Northeast Corridor from Boston to Washington, aiming for 3-3.5 hour end-to-end trip times. And as the Corridor is completed, the priority should be extensions in all directions: south to Atlanta, north to Springfield and (by legacy rail) Portland, west to Pittsburgh and Cleveland, northwest to Upstate New York and Toronto.

The model

To quantify the benefits, I’m going to look purely at railroad finances: construction costs go out, annual profits go in. Intercity high-speed rail pretty much universally turns an operating profit, the question is just how it compares with interest on capital construction. For this, in turn, we need to estimate ridership. Here is an illustrative photo of the sophistication of the model I am using:

In the picture: someone who gets on the train without letting you get off first. Credit: William O’Connor.

The theoretical model for ridership is called a gravity model: ridership between two cities of populations Pop_A and Pop_B at distance d is proportional to

\mbox{Pop}_{A}\cdot\mbox{Pop}_{B}/d^{2}.

However, two complications arise. First of all, there are some diseconomies of scale: the trip time from the train station to one’s ultimate destination is likely to be much higher if the city is as huge as Tokyo or New York than if it is smaller. Empirically, this can be resolved by raising the populations of both cities to an exponent slightly less than 1; on the data I have, which is Japanese (east and west of Tokyo), Spanish (Madrid-Barcelona, Madrid-Seville), and French (see post here – all its sources link-rotted), the best exponent looks like 0.8.

And second, at short distance, the gravity model fails for two reasons: first, access time dominates so in-vehicle time is less important, and second, passengers drive more and take fast trains less. In fact, on the data I’m most certain of the quality of – that from Japan – ridership seems insensitive to distance up to and beyond the distance of Tokyo-Osaka, which is 515 km by Shinkansen. Tokyo-Hiroshima, 821 km and 3:55 by Shinkansen, underperforms Tokyo-Osaka by a factor of about 1.6 if the model is \mbox{Pop}_{A}^{0.8}\cdot\mbox{Pop}_{B}^{0.8} if we lump in air with rail traffic; of course, air travel time is incredibly insensitive to distance over this range, so it may not be fair to do so. French data taken about 3 hours out of Paris overperforms the mid-distance Shinkansen, although that’s partly an artifact of lower fares on the TGV.

To square this circle, I’m going to make the following assumption: the model is,

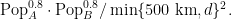
\mbox{Pop}_{A}^{0.8}\cdot\mbox{Pop}_{B}^{0.8}/\min\{500 \mbox{ km}, d\}^{2}.

If the populations of the two metro areas so connected are in millions then the best constant for the model is 75,000: that is, take out the number the formula spits, multiply by 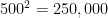500^{2} = 250,000 to get rid of the denominator at low d, multiply by 0.3, and make that your annual number of passengers in millions.

Finally, operating costs are set at $0.05/seat-km or $0.07/passenger-km, which is somewhat lower than on the TGV but realistic given how overstaffed and peaky the TGV is. This is inclusive of the capital costs of rolling stock, but not of fixed infrastructure. Fares are set at $0.135/passenger-km, a figure chosen to make New York-Boston and New York-Washington exactly $49 each, but on trips longer than 770 km, the fares rise more slowly so that profit is capped at $50/trip. Of note, Shinkansen fares are about $0.23/p-km on average, so training data on Shinkansen fares for a network that’s supposed to charge lower fares yields conservative ridership estimates; I try to be conservative since my model is, as the picture may indicate, not the most reliable.

The model on the Northeast Corridor

The Northeast Corridor connects four metropolitan areas: Boston (8 million people), New York (22), Philadelphia (7), Washington (10). All populations cover combined statistical areas, just as the metropolitan area definitions in Japan are expansive and include faraway exurbs. In the Northeast, the CSAs lump together some independent metro areas, such as Baltimore-Washington, but the largest of the subsidiary metro areas, including Baltimore, Providence, New Haven, and Trenton, are along the Northeast Corridor and would get their own stations.

The distances are 360 km Boston-New York, 140 km New York-Philadelphia, 220 km Philadelphia-Washington. I am not going to take into account subsidiary stations in passenger-km calculations, for simplicity’s sake. Splitting Baltimore apart from Washington would actually raise ridership by a little, first because the 0.8 exponent means that combining metro areas reduces ridership, and second because Boston-bound ridership is higher if we assume the destination is a little bit closer.

The highest-ridership city pair is New York-Washington. Per the formula above, we get

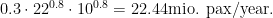
0.3\cdot 22^{0.8}\cdot 10^{0.8} = 22.44 \mbox{mio. pax/year.}

By the same formula, New York-Boston is 18.77 million, New York-Philadelphia is 16.87 million, Washington-Philadelphia is 8.98 million, and Boston-Philadelphia is 7.51 million. All of these are within the 500 km limit in which we assume distance doesn’t matter. Finally, Boston-Washington is

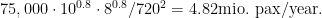
75,000\cdot 10^{0.8}\cdot 8^{0.8}/720^{2} = 4.82 \mbox{mio. pax/year.}

Overall, this is 79.4 million annual passengers, excluding shorter-distance commuter travel like New York-New Haven. Taking distance traveled into account, this is 26.4 billion annual p-km, generating $1.7 billion of operating profit. What I think it should cost to generate this service is investments that, with good value engineering that has been missing from all plans in the last 12 or so years, should cost in the low teens, say $13 billion. If costs can be held to $13 billion, or just less than $20 million per kilometer for a line of which about two-thirds of the physical infrastructure is good enough, then the financial return on investment is 13%. Not bad.

Of note, traffic density is fairly symmetric at the two ends. At the southern end, between Philadelphia and Washington, total traffic density is 36.24 million passengers per year; at the northern end, between New York and Boston, it is 31.1 million. So there should be some extra trains just for New York-Philadelphia, where the expected traffic density is 51.64 million – perhaps ones diverting west to inland Pennsylvania, perhaps interregional trains making an extra stop or two running 5-10 minutes slower than the trains to Washington – but otherwise trains should run on the entire corridor from Boston to Washington.

Also of note, I don’t expect much peakiness on the line – probably none outside the New York-Philadelphia segment. Short-distance lines, including New York-New Haven and New York-Philadelphia, have a rush hour peak in travel. But longer-range intercity lines generate weekend leisure travel and same-day business travel, both of which tend to peak outside the regular rush hour; TGV traffic, heavily weighted toward longer-range city pairs, peaks on Friday and Sunday, with weaker weekday ridership to balance it out. The Northeast Corridor thus benefits from mixing cities at various ranges, with the various peaks mostly canceling each other out. It’s plausible to get away with running service at a regular interval of every 15 minutes all day, with extra trains on New York-Philadelphia.

The Northeast Corridor and Metcalfe’s law

Two examples of Metcalfe’s law in action can be found on the corridor, one for an expansion and one for a contraction.

The contraction would be to ignore Boston and just focus on New York-Washington. The traffic density is higher there, for one. Moreover, no extensive civil infrastructure is required, only some small fixes in Maryland and New Jersey, a rebuild of the catenary, and rebuilds of the station throat interlockings. However, this is less prudent than it seems, because Boston doesn’t just generate traffic on New York-Boston, but also on New York-Washington, on trains bound from points south of New York to Boston.

If we exclude Boston, we have just three city pairs on what is left: New York-Washington, New York-Philadelphia, Washington-Philadelphia. They total 48.3 million passengers per year and 12.4 billion p-km – in other words, slightly less than half the p-km of the entire line including Boston. What’s more, there’s an extra fudge factor, not modeled in my ridership screen, coming from peakiness: a shorter line is one with a more prominent rush hour peak, as the longer trips on Boston-Washington are not included, and this ends up requiring more rush hour-only equipment and increases operating expenses per p-km.

The expansion is, in this section, one that is almost part of the Northeast Corridor today: New Haven-Springfield. The line is unelectrified today despite substantial investment by Connecticut, which like other American states is allergic to rail electrification for reasons that are beyond me. Speeds today are low, even though the right-of-way is straight. However, investment in bypasses and in speedups on the highest-quality legacy segment is possible, and would connect Hartford and Springfield to New York and points south.

The Hartford-Springfield region has 2 million people, and Springfield is 100 km from New Haven and 210 from New York. We apply our usual model and get New York-Springfield ridership of 6.19 million, Philadelphia-Springfield ridership of 2.48 million, and Washington-Springfield ridership of 3.3 million. In passenger-kilometers, these three city pairs amount to 1.3 billion, 620 million, and 1.55 billion respectively, for a total of 3.47 billion, which I will round to 3.5 billion to avoid giving the impression that the model is reliable to 3 significant figures (or even 2, to be honest).

So we have 3.5 billion additional p-km for just 100 km of new construction, or 35 million p-km per km of construction. Note that the expected density on New Haven-Springfield based on the model is just 12 million passengers – the remaining p-km are on the core Northeast Corridor, as passengers from New York and points south travel on a portion of the corridor to get up to the branch to Springfield. So even though the expected traffic is very light, the impact on revenue per kilometer of construction is comparable to that of the base corridor. If costs can be held to $2 billion, which is low-end for an entirely greenfield line but reasonable for service that would partly run on the existing legacy line, then the return on investment is $0.065*3.5/$2 = 11%, almost as high as on the base Northeast Corridor.

Further extensions

Portland (0.7)

To the north, it is valuable to run upgraded legacy trains between Boston and Portland, with a short connection to high-speed trains at South Station. Estimating ridership and revenue there is dicier, because the trains are slower and the data is trained on high-speed trains. We assume 190 km of revenue, as is the current length of the line. But costs and the ridership-suppressing effect of distance are charged at 350 km, roughly scaled for time.

With this in mind, ridership on Boston-Portland is 1.19 million, ridership on New York-Portland is 1.33 million, ridership on Philadelphia-Portland is 0.37 million, and ridership on Washington-Portland is 0.31 million. In total, this is about 1.5 billion p-km, of which 45 million, all from Washington, are beyond the 770 km at which fares are $0.135/km and are charged at the lower rate of $0.07/km. Altogether it’s around $200 million a year in revenue. Costs are around $140 million, including extra costs for service south of Boston. Operating profits are fairly low, but Boston-Portland legacy trains don’t cost per km nearly as much as high-speed rail; electrification and some track work can be done for maybe $600 million, for an ROI of 10%.

Of course, this ROI does not exist without high-speed rail the Northeast Corridor and without the separately-charged North-South Rail Link for local and regional trains. Like other tails, Boston-Portland is valuable once the mainline preexists – it isn’t so great on its own.

The South

The route from Washington to Atlanta has a sequence of cities roughly following the I-85 corridor. They are small and sprawly, but are still valuable to connect thanks to Metcalfe’s law. These include Richmond (1, and 180 km from Washington), Raleigh (2, and 240 km from Richmond), the Piedmont Triad (1.6, 120 km), Charlotte (2.6, 150 km), Greenville (1.4, 160 km), and finally Atlanta (7, 230 km).

The line is long, 50% longer than the Northeast Corridor. With quite sprawly cities in North Carolina and few good rights-of-way, takings and viaducts are needed and would raise construction costs, to perhaps $30 billion. Moreover, there is probably an intercity rail ridership penalty because these cities do not have public transportation; the model does not incorporate such a penalty, which should be regarded as a risk with investments made appropriately. And yet, each city in sequence generates ridership on the line to its north, creating decent ROI if we assume the model applies literally.

Take Richmond. It’s a small city, generating 1.89 million annual riders to Washington, 1.42 million to Philadelphia, 3.05 million to New York, 0.49 million to Boston. But this is 2.9 billion p-km for just 180 km of new construction, and nearly all of these p-km are chargeable at the full rate, giving us a total of $190 million in annual operating profit. If construction can be kept to $5 billion, this is just short of 4% ROI, which is not amazing but is decent for how small Richmond is compared with the cities to its north.

This calculation cascades farther south. We have the following table of ridership levels, in millions of annual passengers as always:

City N\City S Richmond Triangle Triad Charlotte Greenville Atlanta
Boston 0.49 0.66 0.36 0.43 0.21 0.58
New York 3.05 3.14 1.6 1.73 0.79 2.03
Philadelphia 1.42 1.87 0.9 0.92 0.41 1.13
Washington 1.89 3.3 2.36 2.13 0.86 1.92
Richmond – 0.64 0.44 0.62 0.22 0.44
Triangle – – 0.76 1.12 0.68 1.42
Triad – – – 0.94 0.57 1.78
Charlotte – – – – 0.84 3.06
Greenville – – – – – 1.9

This leads to the following operating profits, in millions of dollars per year:

City N\City S Richmond Triangle Triad Charlotte Greenville Atlanta
Boston 24.5 33 18 21.5 10.5 29
New York 107.06 157 80 86.5 39.5 101.5
Philadelphia 36.92 77.79 44.46 46 16.5 56.5
Washington 22.11 90.09 82.84 95.53 43 96
Richmond – 9.98 10.3 20.55 9.58 88
Triangle – – 5.93 19.66 19.01 60.92
Triad – – – 9.17 11.49 62.48
Charlotte – – – – 8.74 77.57
Greenville – – – – – 19.76

This totals to $1.8 billion a year, or an ROI of 6%. This is not a safe number – a hefty share of the figure comes from city pairs that trains would connect in 3.5+ hours, like New York-Charlotte, Washington-Atlanta, and even the 5.5-hour New York-Atlanta, in which range the model has essentially two data points (Tokyo-Hiroshima, Paris-Nice). Another noticeable share comes from intra-South connections, in which neither city in the pair has a strong center or a public transport network to connect the station with destinations.

But thankfully, because this line can build itself up by accretion of extensions, starting with Washington-Raleigh and seeing how ridership holds up would not create a white elephant, just missed benefits if the model is in fact correct.

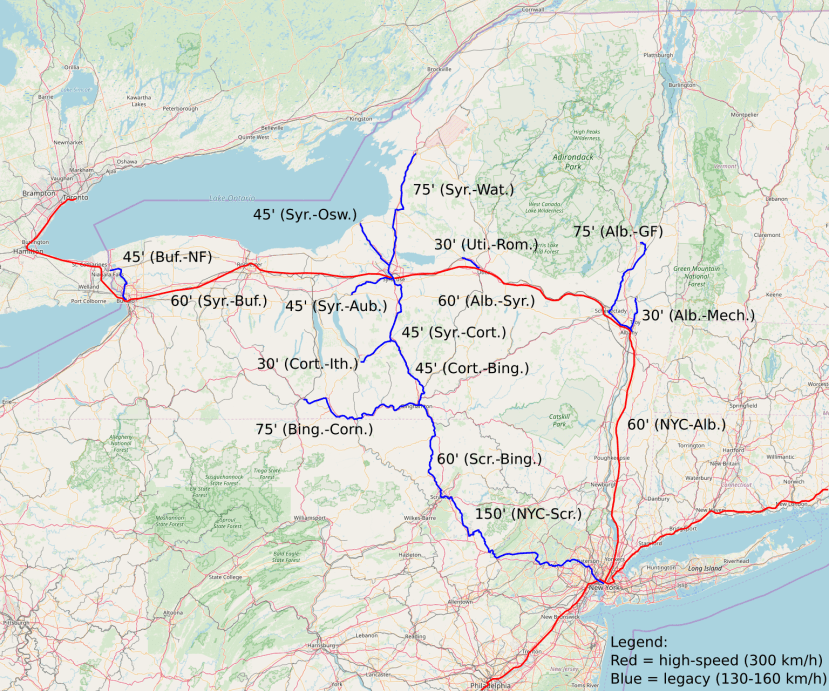
Harrisburg (0.7), Pittsburgh (2.5), and Cleveland (3)

The Keystone corridor is an interesting example of a branch that gets stronger if it is longer. The reason for this is that Harrisburg is pretty small, and Harrisburg-Pittsburgh requires painful tunneling across the Appalachians. Philadelphia-Harrisburg is 170 km and can probably be done for $4 billion; Harrisburg-Pittsburgh is 280 km and, as a pure guess, requires around 40 kilometers of tunnel, let’s say $14 billion. Pittsburgh-Cleveland is 200 km and may require some tunneling near the Pittsburgh end to bypass suburban sprawl without good rights-of-way, but not too much – figure it for $6 billion.

For the benefits, we make a table similar to that for the South, but smaller. Of note, Washington-Harrisburg is 390 km and about 1:45, and costs accordingly to operate, but can only charge for 220 km, or $30, barely more than breakeven rate, because the straight line distance is short and high fares may not be competitive with driving on I-83. The straight line distance is even shorter than 220, about 190 via Baltimore, but Washington-Philadelphia is 220. Trains from Washington are assumed to earn the usual marginal profit west of Harrisburg, $0.065/km up to a maximum of $50, which is not reached even in Cleveland.

Finally, note that Cleveland has a big difference between the population of the core metro area (2 million) and the combined one (3.5), like Boston and Washington. Here we don’t take the bigger population but split the difference, since the biggest subsidiary regions in the combined area, Akron and Canton, could plausibly be on the line – and if they’re not then the line can serve Youngstown (0.7), and then 2^{0.8} + 0.7^{0.8} \approx 3^{0.8}. Note, finally, that Boston-Cleveland is faster via Albany and Buffalo, so the line through Pittsburgh is not considered even if it is built first.

City E\City W Harrisburg Pittsburgh Cleveland
Boston 0.66 0.91 –
New York 2.67 5.32 3.43
Philadelphia 1.07 2.96 2.03
Washington 1.42 2.19 1.51
Harrisburg – 0.47 0.54
Pittsburgh – – 1.5

And as before, using the special malus for the roundabout Washington-Harrisburg route, we have the following operating revenues in millions of annual dollars:

City E\City W Harrisburg Pittsburgh Cleveland
Boston 28.74 45.5 –
New York 53.8 204.02 171.5
Philadelphia 11.82 86.58 85.77
Washington 3.41 45.11 50.74
Harrisburg – 8.55 16.85
Pittsburgh – – 19.5

Note that the relatively easy to build segment to Harrisburg only generates $98 million in operating profit on $4 billion in construction costs, just less 2.5% ROI – Harrisburg is almost as big as Richmond, but it’s a branch and not a direct extension. Then Pittsburgh generates $390 million on $14 billion, or 2.8%. But Cleveland, easier to build to and bigger than Pittsburgh, manages to generate $344 million on $6 billion, finally a respectable ROI of 6%.

The northern cross

What may be caled the northern cross or the Albany cross – that is, a cruciform system consisting of lines from Albany to New York, Boston, Montreal, and Toronto – is an interesting case of a system where Metcalfe’s law again applies and encourages going big rather than small.

To apply the model, we make a crucial assumption: the same formula calibrated to domestic travel works internationally. Eurostar severely underperforms it – it has 10 million annual riders, of whom around 7-8 million go between London and Paris, where the formula predicts 18 million. Eurostar fares are very high, and has mandatory security theater and a slow boarding process that breaks down at peak travel time, and this may be enough to explain the low ridership. But then again, domestic TGVs overperform the model.

We also make a secondary assumption: fares charged are for actual distance traveled, even though the New York-Toronto routing isn’t the most direct.

We start with the New York-Toronto leg by itself. It connects New York to Albany (1.2, 220 km), Utica (0.3, 140 km from Albany), Syracuse (0.8, 80 km), Rochester (1.1, 120), Buffalo (1.2, 110), and Toronto (8, 160 km). Toronto’s metro population ranges between 6 million and 9 million depending on definition, and the high-end figure of 8 million is justifiable by the fact that Niagara Falls and Hamilton are on the line.

City S\City N Albany Utica Syracuse Rochester Buffalo Toronto
Washington 1.63 0.35 0.62 0.6 0.52 1.76
Philadelphia 1.65 0.54 0.88 0.78 0.63 2
New York 4.12 1.36 2.67 3.06 2.29 6.81
Albany – 0.13 0.26 0.37 0.4 1.23
Utica – – 0.09 0.12 0.13 0.6
Syracuse – – – 0.24 0.26 1.19
Rochester – – – – 0.37 1.71
Buffalo – – – – – 1.83

And in operating profit:

City S\City N Albany Utica Syracuse Rochester Buffalo Toronto
Washington 61.45 16.38 31 30 26 88
Philadelphia 38.61 17.55 33.18 35.49 31.5 100
New York 58.92 31.84 76.36 109.4 99.73 340.5
Albany – 1.18 3.72 8.18 11.7 48.77
Utica – – 0.47 2.03 3.13 18.33
Syracuse – – – 1.87 3.89 30.17
Rochester – – – – 2.65 30.01
Buffalo – – – – – 19.03

New York-Albany should cost maybe $5 billion to build and generates $160 million a year in operating profit, just 3.2%. But Albany-Buffalo, for around $11 billion extra, generates $580 million, about 5.2%. And then Buffalo-Toronto, assuming no international penalty, should cost on the order of $3 billion (much of the line in the Toronto suburbs automatically follows from the ongoing electrification project) and generate $670 milion. So the last segment, Buffalo-Toronto, returns around 20% if New York-Buffalo preexists; even if there’s a serious international malus, the ROI is very high. Everything combined is around 7%.

None of this is robust. The model handwaves the forced transfer at Penn Station – through-service from points south to Albany and points north would be excellent given expected traffic levels, but the approaches to both Albany and Philadelphia point west. The model also assumes New York-Toronto fares are in line with rail distance, even though the route is 50% longer by rail than by air. Finally, it assumes no international penalty. A 7% ROI is robust to any one of these assumptions failing, but if all fail, the route drops in profitability.

Or, rather, the base route does. Just as completing Buffalo-Toronto makes New York-Buffalo seem far stronger, so do the two additional legs of the northern cross strengthen the initial Empire Corridor. Here’s the Boston-Albany leg, at 260 km, with Springfield at kp 135, recalling that Hartford and Springfield count as one region of 2 million:

City W\City E Boston Springfield
Springfield 2.76 –
Albany 1.83 0.6
Utica 0.6 0.2
Syracuse 1.32 0.44
Rochester 1.19 0.56
Buffalo 0.91 0.46
Toronto 2.76 1.28

And in revenue:

City W\City E Boston Springfield
Springfield 24.22 –
Albany 30.93 4.88
Utica 15.6 3.45
Syracuse 41.18 9.87
Rochester 46.41 16.93
Buffalo 45.5 17.19
Toronto 138 61.15

$450 million a year, of which nearly half comes out of connecting Toronto to Massachusetts and Hartford, is not a lot, but then constructing 260 km of high-speed rail is not that expensive either; my best guess is around $7 billion, with some tunnels between Springfield and the summit to the west but also some approaches at both ends that would already exist. This is 6.4% ROI, which is better than New York-Toronto gets without the assistance of Philadelphia and Washington even though that route connects to a bigger city and requires less tunneling.

The final leg of the northern cross is to Montreal (4, 370 km from Albany), and is the most speculative. If the model has an international malus, it may well apply here, crossing not just a national border but also a linguistic one. It may apply with no or limited penalty, if the underperformance of Eurostar can be ascribed entirely to fares; but if it applies and is serious, then there is less cushion for mistakes than there is for trains to Toronto. The only intermediate city is Burlington (0.2, kp 220 from Albany), which exists largely for state-level completeness. Note also that Buffalo-Montreal is faster via Toronto and is thus omitted, while Buffalo-Burlington would have third-order impact.

City ESW\City N Burlington Montreal
Washington 0.2 1.59
Philadelphia 0.29 2.02
New York 0.98 7.74
Albany 0.1 1.05
Boston 0.44 3.02
Springfield 0.14 1.58
Utica 0.03 0.33
Syracuse 0.06 0.49
Rochester 0.07 0.5
Burlington – 0.25

And in operating revenue:

City ESW\City N Burlington Montreal
Washington 10 31.8
Philadelphia 10.93 95.85
New York 28.03 296.83
Albany 1.43 25.25
Boston 13.73 123.67
Springfield 3.14 50.84
Utica 0.7 10.94
Syracuse 1.72 18.79
Rochester 2.55 23.08
Burlington – 2.44

This is $750 million a yeer, of which Burlington furnishes about 10%, and New York-Montreal about 40%. This isn’t bad ROI – about $10 billion is a reasonable construction cost – but since 90% of it is about Montreal, any serious international or interlinguistic penalty leads to a big drop in profitability. Worse, if traffic drops, there may be a frequency-ridership spiral – I am writing timetables assuming half-hourly frequency, which is just enough for the model’s projected 18 million passengers per year, but if ridership is off by a factor of more than 2, then hourly frequencies start taking a bite out of the nearer markets and trains start running less full.

Lines that do not touch the Northeast Corridor

In the previous sections, I’ve argued in favor of building out a high-speed rail network out of the Northeast Corridor, on the grounds that extensions would be profitable toward Pittsburgh-Cleveland, Montreal, Buffalo-Toronto, and Atlanta. What about other lines?

The answer is that lines that do not feed into the Northeast somehow are a lot weaker. California can get decent ridership out of Los Angeles-San Francisco and thence extensions to Sacramento and San Diego are pretty strong, but the traffic density per the model is both well below California HSR Authority projections and well below the Northeast Corridor.

And it gets worse in parts of the country without a Los Angeles-size city anchoring everything. Texas is currently building a Dallas (8)-Houston (7) high-speed line, using private money by Texas Central, a railroad owned by JR Central using Shinkansen technology. The model predicts 7.5 million annual riders between the two regions, and the system’s public ridership projections for the near term are pretty close. Moreover, construction costs are pretty high, $15 billion for 380 km, despite the flat terrain. If the operating costs and fares are what I’m projecting, the financial ROI is 1.2%.

What’s more, Texas can expect ridership to underperform any model trained on European or Japanese cities. Tokyo has the world’s largest central business district, and maintains high density of destinations at a distance of several kilometers from Tokyo Station as well, and 20-something rapid transit lines depending on how one counts feed this center. Paris is smaller but has a strong center and urban rail connections. The provincial cities in both countries are lower-density and have higher car ownership, but that’s still okay, because people from those cities are not driving into the capital. By the same token, trains to New York should not underperform a model trained on Japan, Spain, or France. But Texas is completely different, with very weak centers, no public transportation to speak of, and no walkable cores near the train stations. The penalty for poor public transport connections is likely to be serious.

The situation in the Midwest is more hopeful than in Texas, but still dicey. Chicago just isn’t that big. Yes, it’s about the same size as Paris, but the cities ringing it don’t form neat lines the way Lyon and Marseille are on the same line out of Paris, just with a short spur rather than through-service.

The funniest thing about the Midwest is that high-speed rail construction there may be justifiable as an accretion of western extensions from the Northeast and Keystone Corridors. Cleveland-Detroit (5) is 280 km long, and would put Detroit 1,070 km and slightly more than 4 hours away from New York. The distance penalty is hefty, but 2.81 million annual users is still a lot over such distance, and the $140 million in operating profits get to around 2.5% ROI on construction costs in flat Midwestern land, without taking any other connections into consideration: Chicago-Cleveland, Chicago-Detroit, Philadelphia-Detroit, Pittsburgh-Detroit, New York-Toledo, Washington-Detroit.

Even New York-Chicago is a fairly solid line per the model: it’s 1,340 km and slightly longer than 5 hours, but there is still a lot of travel volume between the two cities, mostly by air. The model says 3.12 annual high-speed rail riders, somewhat fewer than the current O&D flight volume (4.68 million annualized from 2018 Q2), which is believable by comparison with Paris-Nice’s mode share (70% air, 30% rail, ignoring all other modes). The required mode share is still more favorable to rail, but the airports in New York and Chicago have more congestion and more delays than in Nice, turning what is a little more than an hour in the air into a three-hour flight schedule.

In contrast, just starting from Chicago-Cleveland (550 km)/Detroit (470 km), without any other connections (and without Pittsburgh-Cleveland), would not be financially great. Ignoring Toledo, the three cities generate 13 million annual riders, 6 billion annual p-km, and $400 million in annual operating income, for a system that would take perhaps $13 billion to construct, perhaps slightly more.

What this means for high-speed rail construction

Metcalfe’s law implies that high-speed rail networks get stronger as they add more nodes, even if those nodes are somewhat weaker than the initial ones. But it gives guideines for how to build such networks more broadly:

  • Don’t cheap out by only building a short segment.
  • Once the initial segment is in place, invest in extending it and building branches off it as soon as possible, in preference to building unconnected segments elsewhere.
  • A relatively empty tail may still be financially successful if it fills a trunk line.
  • Unless all your cities are on one line, try to build a mesh of lines to allow many origin-destination pairs.
  • You’ll always run into a frontier of marginal lines, so value-engineer infrastructure as much as possible to push that frontier forward.
  • Be wary of lines for which the analysis involves extrapolation, for example if neither city has a strong center or usable public transport.

High-speed rail is cheap to run when there’s enough scale to fill trains – high speeds ensure that labor and equipment cost per seat-km are fairly low. This means that self-sustaining profits are viable, and once they’re in place, they can generate further borrowing capacity for rapid expansion.

The limit is not the sky. Beyond a certain point, no realistic value engineering can make lines financially viable. Sometimes the cities are just too small or too far apart. But a realistic limit for the United States is still most likely much farther than anyone proposing immediate investment plans thinks: the Northeast Corridor can generate good returns if investment there is ever done competently, and branches and extensions to smaller and less dense cities are still more viable than they look at first glance.