Bus Stop Consolidation and Blocks

There are arguments over bus stop spacing in my Discord channel. As the Queens bus redesign process is being finalized, there’s a last round of community input, and as one may expect, community board members amplify the complaints of people who reject any stop consolidation on “they’re taking my stop, I’ll have to walk longer” grounds. I wrote about this in 2018, as Eric and I were releasing our proposed Brooklyn bus redesign, which included fairly aggressive consolidation, to an average interstation of almost 500 meters, up from the current value of about 260. I’d like to revisit this issue in this post, first because of its renewed relevance, and second because there’s a complication that I did not incorporate into my formula before, coming from the fact that the city comprises discrete blocks rather than perfectly isotropic distribution of residents along an avenue.

The formula for bus stop spacing

The tradeoff is that stop consolidation means people have to walk longer to the bus stop but then the bus is faster. In practice, this means the bus is also more frequent by a proportionate amount – the resources required to operate a bus depend on time rather than distance, chiefly the driver’s wage, but also maintenance and fuel, since stops incur acceleration and idling cycles that stress the engines and consume more fuel.

The time penalty of each stop can be modeled as the total of the amount of time the bus needs to pull into the stop, the minimum amount of time it takes to open and close the doors, and the time it takes to pull out. Passenger boardings are not included, because those are assumed to be redistributed to other stops if a stop is deleted. In New York and Vancouver, the difference in schedules between local and limited stop buses in the 2010s was consistent with a penalty of about 25 seconds per stop.

The optimum stop spacing can be expressed with the following formula:

\sqrt{d\cdot\frac{\mbox{walk speed}}{\mbox{walk penalty}}\cdot\mbox{stop penalty}\cdot(\mbox{average trip length} + \mbox{average bus spacing})}

To explain in more detail:

  • d is a dimensionless factor indicating how far one must walk, based on the stop spacing; the more isotropic passenger travel is, the lower d is, to a minimum of 2. The specific meaning of d is that if the stop spacing is n, then the average walk is n/d. For example, if there is perfect isotropy, then passengers’ distance from the nearest bus stop is uniformly distributed between 0 and n/2, so the average is n/4, and this needs to be repeated at the destination end, summing to n/2.
  • Walk speed and walk penalty take into account that passengers prefer spending time on a moving bus to walking to the bus. In the literature that I’ve seen, the penalty is 2. Usually the literature assumes the walk speed is around 5 km/h, or 1.4 m/s; able-bodied adults without luggage walk faster, especially in New York, but the speed for disabled people is lower, around 1 m/s for the most common cases.
  • Stop penalty, as mentioned above, can be taken to be 25 s.
  • Average trip length is unlinked; for New York City Transit in 2019, counting NYCT local buses including SBS but not express buses, the average was 3,421 meters.
  • Average bus spacing is the headway between buses on the route measured in units of distance, not speed; it’s expressed this way since the resources available can be expressed in how many buses can circulate at a given time, and then the frequency is the product of this figure with speed. In Brooklyn in the 2010s, this average was 1,830 m; our proposed network, pruning weaker routes, cut it to 1,180. The Queens figure as of 2017 appears similar to the Brooklyn figure, maybe 1,860 m. Summing the average trip length and average bus spacing indicates that passengers treat wait time as a worst-case scenario, or, equivalently, that they treat it as an average case but with a wait penalty of 2, which is consistent with estimates in the papers I’ve read.

In the most isotropic case, with d = 2, plugging in the numbers gives,

\sqrt{2\cdot\frac{1.4}{2}\cdot 25\cdot(3420+1860)} = 430 \mbox{meters}

However, isotropy is more complex than this. For one, if we’re guaranteed that all passengers are connecting to one distinguished stop, say a subway connection point, then consolidating stops will still make them walk longer at the other end, but it will not make them walk any longer at the guaranteed end, since that stop is retained. In that case, we need to set d = 4 (because the average distance to a bus stop if the interstation is n is n/4 and at the other end we’re guaranteed there’s no walk), and the same formula gives,

\sqrt{4\cdot\frac{1.4}{2}\cdot 25\cdot(3420+1860)} = 608 \mbox{meters}

The Queens bus redesign recognizes this to an extent by setting up what it calls rush routes, designed to get passengers from outlying areas in Eastern Queens to the subway connection points of Flushing and Jamaica; those are supposed to have longer interstations, but in practice this difference has shrunk in more recent revisions.

That said, even then, there’s a complication.

City blocks and isotropy

The models above assume that passengers’ origins are equally distributed along a line. For example, here is Main Street through Kew Gardens Hills, the stretch I am most likely to use a New York bus on:

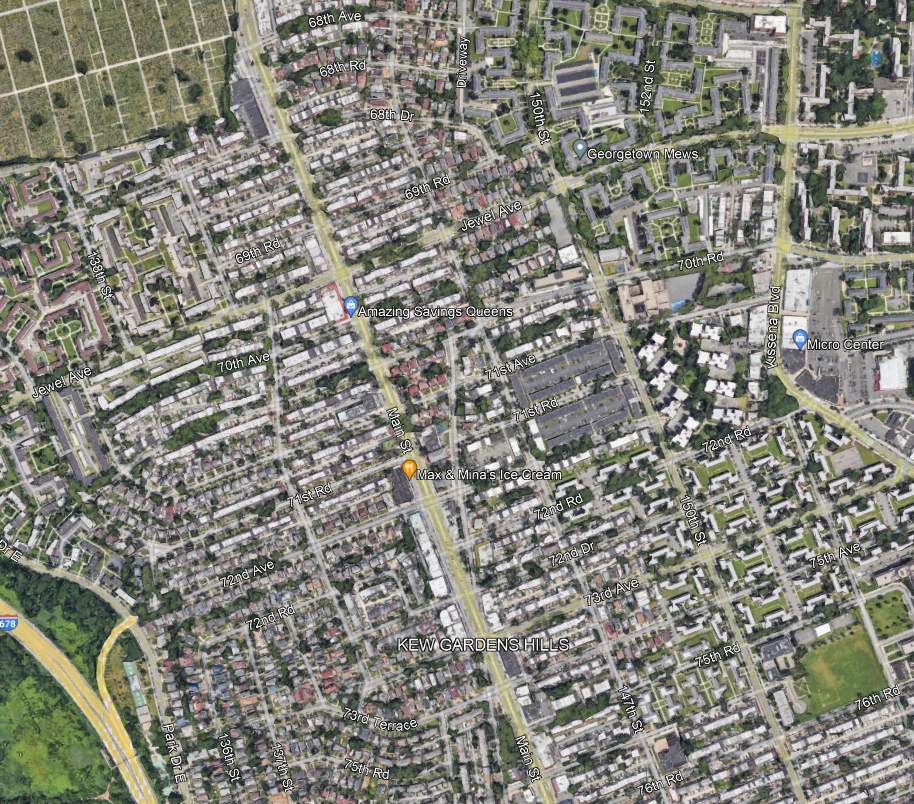
I always take the bus to connect to Flushing or Jamaica, but within Kew Gardens Hills, the assumption of isotropy means that passengers are equally likely to be getting on the bus at any point along Main Street.

And this assumption does not really work in any city with blocks. In practice, neighborhood residents travel to Main Street via the side streets, which are called avenues, roads, or drives, and numbered awkwardly as seen in the picture above (72nd Avenue, then 72nd Road, then 72nd Drive, then 73rd Avenue, then 75th Avenue…). The density along each of those side streets is fairly consistent, so passengers are equally likely to be originating from any of these streets, for the most part. But they are always going to originate from a side street, and not from a point between them.

The local bus along Main, the Q20, stops every three blocks for the most part, with some interstations of only two blocks. Let’s analyze what happens if the system consolidates from a stop every three blocks, which is 240 meters, to a stop every six, which is 480. Here, we assume isotropy among the side streets, but not continuous isotropy – in other words, we assume passengers all come from a street but are equally likely to be coming from any street.

With that in mind, take a six-block stretch, starting and ending with a stop that isn’t deleted. Let’s call this stretch 0th Street through 6th Street, to avoid having to deal with the weird block numbering in Kew Gardens Hills; we need to investigate the impact of deleting a stop on 3rd Street. With that in mind: passengers originating on 0th and 1st keep going to 0th Street and suffer no additional walk, passengers originating on 5th keep going to 6th and also suffer no additional walk, passengers originating on 2nd and 4th have to walk two blocks instead of one, and passengers originating on 3rd have to walk three blocks instead of zero. The average extra walk is 5/6 of a block. This is actually more than one quarter of the increase in the stop spacing; if there is a distinguished destination at the other end (and there is), then instead of d = 4, we need to use d = 3/(5/6) = 3.6. This shrinks the optimum a bit, but still to 576 m, which is about seven blocks.

The trick here is that if the stop spacing is an even number of blocks, then we can assume continuous isotropy – passengers are equally likely to be in the best circumstance (living on a street with a stop) and in the worst (living on a street midway between stops). If it’s an odd number of blocks, we get a very small bonus from the fact that passengers are not going to live on a street midway between stops, because there isn’t one. The average walk distance, in blocks, with stops every 1, 2, 3, … blocks, is 0, 0.5, 2/3, 1, 1.2, 1.5, 12/7, 2, … Thus, ever so slightly, planners should perhaps favor a stop every five or seven blocks and not every six, in marginal cases. To be clear, the stop spacing on each stretch should be uniform, so if there are 12 blocks between two distinguished destinations, there should be one intermediate stop at the exact midpoint, but, perhaps, if there are 30 blocks with no real internal structure of more or less important streets, a stop should be placed every five and not six blocks, especially if destinations are not too concentrated.

Fares on High-Speed Trains

American journalists sometimes ask me to discuss high-speed rail fares. I’ve written from time to time about how Northeast Corridor fares are significantly higher than French, German, and Japanese high-speed rail fares, but the links to this information are never in the same place. The purpose of this post is to collect all the links together for easy retrieval, with updates to the 2020s whenever possible. Unfortunately, international high-speed rail fares connecting to France are also much higher than domestic ones, which contributes to the poor ridership of those trains relative to city size.

France

ARAFER releases statistics annually. The most recent year for which there is data is 2022; here’s the report in French, and here’s a summary in English. The relevant information is in sections 5-6. The TGV system including international trains averages fare revenue of 6,213M€ for 61 billion passenger-km; in English this is called “non-PSO,” since these are the profitable trains that SNCF runs outside the passenger service obligation system for money-losing slow trains. This works out to 0.102€/p-km. The PPP rate these days is about 1€ = $1.45, making this about $0.15/p-km.

The split between domestic and international trains is large, and the French report has the domestic trains as just 0.093€/p-km, taking a weighted average from pp. 23 and 31. Nominal fares per p-km on domestic TGVs were down 4% from 2019 to 2022, despite 7.5% cumulative inflation over this period.

The international trains, in contrast, are much more expensive: the report doesn’t give exact numbers, but from some weighted averaging and graph eyeballing it looks like it’s around 0.17€/p-km. The all-high-speed international trains – Eurostar and Thalys – are more expensive than the trains running partly at low speed in Germany and Switzerland, like Lyria; this big difference in fares helps explain their disappointing ridership. Domestic TGVs run from Paris to Lyon 28 times on the 5th of June this year, counting only trains to Lyon Part-Dieu or Perrache, which do not continue onward, and not counting trains that stop at Saint-Exupéry on their way to points south, and those trains are rather full 16-car bilevels. In contrast, on the same day I only see 16 Eurostars from London to Paris. This is despite the fact that London is a far larger city than Lyon, and the in-vehicle travel time is only moderately longer.

Germany

Germany lacks France’s neat separation of low- and high-speed trains. The intercity rail network here is treated as a single system, and increasingly all trains are ICEs even if they spend the majority of the trip on legacy lines at a top speed of 200 km/h.

Overall intercity rail passenger revenue here was 5.1 billion € in 2022; the expression to look for is “SPFV.” Ridership was 42.9 billion p-km per a DB report of 2022-3, PDF-p. 7, averaging 0.119€/p-km, which is $0.17/p-km in PPP US dollars. 2022 was still slightly below 2019 levels, when ridership was 44.7 billion p-km and fares averaged 0.112€/p-km; the three-year increase was less than the cumulative inflation over this period, which was 10.3%.

Japan

Japanese fares are higher than European fares on high-speed rail. JR East’s presentation from 2021, showing depressed ridership during the pandemic (p. 50), reports ¥189.6 billion in Shinkansen revenue on 7.95 billion p-km, or ¥23.8/p-km, and projects recovery to ¥428.9 billion/17.313 billion p-km by 2022, or ¥24.8/p-km. JR Central’s 2020 report says (p. 37) that its Shinkansen service got ¥1.2613 trillion in revenue in the year ending March 2020 on 54.009 billion p-km, or ¥23.4/p-km. JR West’s 2020 factsheets for revenue and ridership show ¥457 billion/21.338 billion p-km in 2019, or ¥21.4/p-km.

The PPP rate for 2020-1 was $1 = ¥100. Taking 9% dollar inflation from 2020 to 2022 into account, this is, in 2022 prices, around $0.25/p-km.

Northeast Corridor

Amtrak publishes monthly performance reports; the fiscal year is October-September, so the September reports, covering an entire fiscal year, are to be preferred. Here are 2022 and 2023; 2022 still shows a considerable corona depression, unlike in France and Germany. The 2023 report shows that Northeast Corridor revenue splits as $495.9 million/581.1 million p-miles Acela, or $0.53/p-km, and $768.2 million/1.6269 billion p-miles Regional, or $0.293/p-km Regional. Altogether, this is $0.356/p-km, which is nearly 50% higher than the Shinkansen, 2.1 times as expensive as the ICE, and 2.4 times as expensive as the TGV.

Discussion

High operating costs on Amtrak are the primary reason for the premium fares. The mainland JRs are all highly profitable; DB Fernverkehr is profitable, as is the TGV network (though SNCF writ large isn’t, the slow intercities falling under the PSO rubric). All five companies pay track access charges for the construction of high-speed rail infrastructure; the ARAFER report goes over these charges in France and a selection of other European countries, designed to prevent state subsidies to intercity rail operations through underpriced track access, since track construction is always done by the state but operations may be done by a private operator or a foreign state railway. The Northeast Corridor is profitable as well – Amtrak doesn’t have to pay track access charges, but the access charges for legacy 19th-century lines would not be significant. However, if Amtrak charged European fares or even Japanese ones, it wouldn’t be. Northeast Corridor rail operations in fiscal 2023 earned $1.266 billion in passenger revenue plus $28.5 million in non-ticket revenue but spent $1.0917 billion, or $0.307/p-km.

A portion of the Amtrak cost premium also comes from adversarial profit maximization, also seen on Thalys and Eurostar. The domestic TGVs and ICEs aim at making a base rate of profit while providing a service for the general public; SNCF doesn’t apply the same logic to Thalys and Eurostar and instead aims at serving only business trips to avoid the possibility of extracting less than maximum fares from international travelers. On Amtrak, the need to subsidize the rest of the system has increased Northeast Corridor fares, though to be clear, in fiscal 2023 the operating margin was small enough that this is at most a secondary factor. Performance reports from the 2000s and 10s showed a larger operating margin, but criticism from advocacy groups centering non-Northeast Corridor passengers alleging that Amtrak accounting was making the Northeast Corridor look better and the night trains look worse led to a recalculation, used in the most recent reports, in which Northeast Corridor operations still turn out to be profitable but not by a large margin.

American Myths of European Poverty

I occasionally have exchanges on social media or even in comments here that remind me that too many people in the American middle class believe that Europe is much poorer than the US. The GDP gap between the US and Northern Europe is small and almost entirely reducible to hours worked, but the higher inequality in the US means that the top 10-20% of the US compare themselves with their peers here and conclude that Europe is poor. Usually, it’s just social media shitposting, for example about how store managers in the US earn the same as doctors in Europe. But it becomes relevant to public transit infrastructure construction in two ways. First, Americans in positions of authority are convinced that American wages are far higher than European ones and that’s why American construction costs are higher than European ones. And second, more broadly, the fact that people in positions of authority really do earn much more in the US than here inhibits learning.

The income gap

The United States is, by a slight amount, richer than Northern Europe, which for the purposes of this post comprises the German-speaking world, the Nordic countries, and Benelux. Among the three largest countries in this area, Germany is 16.5% poorer than the US, the Netherlands 8.3% poorer, Sweden 14.3%. This is more than anything an artifact of shorter working hours – Sweden has an ever so slightly larger GDP per hour worked, the other two are 6-7% poorer per hour worked. All three countries have a much higher 15-64 labor force participation rate than the US, but they’re also older, which in the case of Germany actually gets its 15+ rate to be a hair less than the US’s. But there’s much more part-time work here, especially among women, who face large motherhood penalties in German society (see figures 5-7 in Herzberg-Druker, and Kleven et al). Germany is currently in full employment, so it’s not about hidden part-time work; it’s a combination of German-specific sexism and Europe-wide norms in which workers get around six weeks of paid vacation per year.

One implication of the small gap in income per hour is that wages for the same job are likely to be similar, if the jobs pay close to the mean wage. This is the case for tunnel miners, who are called sandhogs in the United States: the project labor agreements in New York are open – the only case in which itemized costs are publicly available – and showcase fully-laden employment costs that, as we document in our construction costs reports, work out to around $185,000/year in 2010 prices; there is a lot of overstaffing in New York and it’s disproportionately in the lower-earning positions, and stripping those, it’s $202,000/year. I was told that miners in Stockholm earn 70,000 kronor/month, or about $100,000/year in PPP terms (as of 2020-1), and the fully-laden cost is about twice that; a union report from the 2000s reports lower wages, but only to about the same extent one would expect from Sweden’s overall rate of economic growth between then and 2021. The difference at this point is second-order, lower than my uncertainty coming from the “about” element out of Sweden.

While we’re at it, it’s also the case for teachers: the OECD’s Education at a Glance report‘s indicator D3 covers teacher salaries by OECD country, and most Northern European countries pay teachers better than the US in PPP terms, much better in the case of Germany. Teacher wage scales are available in New York and Germany; the PPP rate is at this point around 1€ = $1.45, which puts starting teachers in New York with a master’s about on a par with their counterparts in the lowest-paying German state (Rhineland-Pfalz). New York is a wealthy city, with per capita income somewhat higher than in the richest German state (Bavaria), but it’s not really seen in teacher pay. I don’t know the comparative benefit rates, but whenever we interview people about European wage rates for construction, we’re repeatedly told that benefits roughly double the overall cost of employment, which is also what we see in the American public sector.

The issue of inequality

American inequality is far higher than European inequality. So high is the gap that, on LIS numbers, nearly all Western European countries today have lower disposable income inequality than the lowest recorded level for the US, 0.31 in 1980. Germany’s latest number is 0.302 as of 2021, and Dutch and Nordic levels are lower, as low as 0.26-0.27; the US is at 0.391 as of 2022. If distributions are log-normal (they only kind of are), then from a normal distribution log table lookup, this looks like the mean-to-median income ratios should be, respectively, 1.16 for Germany and 1.297 for the US.

However, top management is not at the median, and that’s the problem for comparisons like this. The average teacher or miner makes a comparable amount of money in the US and Northern Europe. The average private consultant deciding on how many teachers or miners to hire makes more money in the US. A 90th-percentile earner is somewhat wealthier in the US than here, again on LIS number; the average top-1%er is, in relative terms, 50% richer in the US than in Germany (and in absolute terms 80% richer) and nearly three times as rich in the US as in Sweden or the Netherlands, on Our World in Numbers data.

On top of that, I strongly suspect that not all 90th percentile earners are created equal, and in particular, the sort of industries that employ the mass (upper) middle class in each country are atypically productive there and therefore pay better than their counterparts abroad. So the average 90th-percentile American is noticeably but not abnormally better off than the average 90th-percentile German or Swede, but is much better off than the average German or Swede who works in the same industries as the average 90th-percentile American. Here we barely have a tech industry by American standards, for example; we have comparable biotech to the US, but that’s not usually where the Americans who noisily assert that Europe is poor work in.

Looking for things to mock

While the US is not really richer than Northern Europe, the US’s rich are much richer than Northern Europe’s. But then the statistics don’t bear out a massive difference in averages – the GDP gap is small, the GDP gap per hour worked is especially small and sometimes goes the other way, the indicators of social development rarely favor the US, immigration into Western Europe has been comparable to immigration to the US for some time now (here’s net migration, and note that this measure undercounts the 2022 Ukrainians in Germany and overcounts them in Poland).

So middle-class Americans respond by looking for creative measures that show the level of US-Europe income gap that they as 90th-percentile earners in specific industries experience (or more), often dropping the PPP adjustment, or looking at extremely specific things that are common in the US but not here. I’ve routinely seen American pundits who should know better complain that European washing machines and driers are slow; I’m writing this post during a 4.5-hour wash-and-dry cycle. Because they fixate on proving the superiority of the United States to the only part of the world that’s rich enough not to look up to it, they never look at other measures that might show the opposite; this apartment is right next to an elevated train, but between the lower noise levels of the S-Bahn, good insulation, and thick tilt-and-turn windows, I need to concentrate to even hear the train, and am never disturbed by it, whereas American homes have poor sound insulation to the point that street noise disturbs the sleep.

Learning to build infrastructure

The topline conclusion of any American infrastructure reform should be “the United States should look more like Continental Europe, Turkey, non-Anglophone East Asia, and the better-off parts of Latin America.”

If it’s written in the language of specific engineering standards, this is at times acceptable, if the standards are justified wholly internally (“we can in fact do this, here’s a drawing”). Even then, people who associate Americanness with their own career success keep thinking safety, accessibility, and similar issues are worse here, and ask “what about fire code?” and then are floored to learn that fire safety here is actually better, as Stephen Smith of Market Urbanism and the Center for Building constantly points out.

But then anything that’s about management is resisted. It’s difficult to convince an American who’s earning more than $100,000 a year in their 20s and thinks it’s not even that much money because their boss is richer that infrastructure project management is better in countries where the CEO earns as much money as they do as an American junket assistant. Such people readily learn from rich, high-inequality places that like splurging, which are not generally the most productive ones when it comes to infrastructure. Even Americans who think a lot about state capacity struggle with the idea that Singapore has almost as high construction costs as the US; in Singapore, the CEO earns an American salary, so the country must be efficient, right? Well, the MRT is approaching $1 billion/km in construction costs for the Cross-Island Line, and Germany builds 3 km of subway (or decides not to build them) on the same budget and Spain builds 6 km, but Europe is supposedly poor and Americans can’t learn from that.

The upshot is that even as we’re seeing some movement on better engineering and design standards in the United States, resulting in significant cost savings, there’s no movement for better overall management. Consultant-driven projects remain the norm, and even proposals for improving state capacity are too driven by domestic analysis without any attempt at international learning or comparativism. Nor is there any effort at better labor efficiency – management in the US hates labor, but also thinks it’s entirely about overpaid workers or union safety rules, and doesn’t stoop to learn how to build more productively.

The Politics of QueensLink

The abandoned right-of-way of the Rockaway Cutoff, or Rockaway Beach Branch, is an attractive target for reuse by some groups. Area railfans have wanted to do something with it for years, and I was mostly negative about these plans, but more recently, QueensLink has emerged as a serious plan to extend the subway along the Rockaway Cutoff, to connect neighborhoods in southwestern Queens to one another and to Manhattan, where current connections do not exist (in the middle) or only serve Midtown Manhattan indirectly and slowly (in the south, via the A train). The right-of-way is wide enough that most of it can also accommodate additional infrastructure, in the case of this plan a bike trail.

The problem is that this more serious plan is still not getting much political play. This is not because of the typical reasons people may think of, such as high costs or NIMBYism. Rather, a competing plan for the same corridor, Queensway, wants to turn it into pure parkland, and is backed by a power broker with opinions and connections. The QueensLink advocates have asked for and been so far refused planning money for an environmental impact statement, which step is in better infrastructure environments apolitical; instead, Mayor Eric Adams is connected with a Queensway backer and thus favors Queensway.

The QueensLink project

QueensLink is a subway extension, with a short tunnel to get from the Queens Boulevard Line’s local tracks to the Rockaway Cutoff. Where there is room, a bike trail is included on the same corridor.

As this is a former rail mainline, the connections to the crossing subway lines are not great – the subway placed stations at major street intersections, leading to long walks at the Jamaica and Liberty Avenue transfers. In contrast, the connection to the LIRR is good: there is no station there today, but there used to be one, and it could be reopened, especially now that the Atlantic Branch is retooling to be more useful for urban service, with more stops, higher frequency, and perhaps integrated fares.

The subway connection makes this proposal viable. I previously criticized a proposal to run commuter rail service on the Cutoff, since it would crowd out the busy LIRR Main Line. In contrast, QueensLink has the new branch using the Queens Boulevard local tracks, which are undersubscribed even at rush hour, to the point that it may even be possible to run three rush hour services on the same tracks and not just two like today. The G doesn’t run to Forest Hills, for good reason, but the new service would vacate space at the Forest Hills terminal of the local tracks to the point that it could potentially be viable.

At the Transportation and Land Use program at Marron, we’re building tools to estimate not just costs for public transit construction but also ridership, and it’s likely that QueensLink will be next on our agenda right after the Interborough Express. I can’t give more than first-order estimates now, but it’s notable that the closest parallel bus corridor, Woodhaven, has high ridership: it carries four local or SBS routes and four express routes, with 31,000 weekday boardings among them. Then there’s the possibility of faster service to JFK Airport via QueensLink. It’s not going to be the Second Avenue Subway of Queens by ridership, but because only a short tunnel is needed, it’s not going to come close to Second Avenue Subway in costs either.

QueensLink and Queensway

The alternative to QueensLink isn’t doing nothing, as is usually the case. Some political players have eyed the corridor for a trail project called Queensway. The idea of Queensway is to create more parkland in the area, including a hiking and bike trail; as the map above shows, there is no shortage of parkland there. There’s an obsession of urbanists in the United States with linear parks, in imitation of the High Line; one attempt at imitation even wanted to build a park underground in a former streetcar terminal and called it the Lowline.

I want to dwell on the politics of Queensway, because I know I have a lot of readers in the general neoliberal and rationalist communities, including specifically in New York, and the political support for it is not what their first instinct might be.

Often, it’s the case that public transit projects are supported by broadly developmentalist interest groups, who are also fairly YIMBY, and tend to be rooted in professionals and office workers commuting to city center, and opposed by NIMBYs, who tend to be rooted in longstanding neighborhood residents and small business owners. Neighborhood NIMBYs often like parks, because they’re local improvements; when we studied the Green Line Extension in Boston, we saw some local interest groups demand money for a trail as a precondition to supporting the light rail line.

And this is not at all what is happening with the Rockaway Cutoff. Local interest groups are not consistently anti-QueensLink and pro-Queensway. Some are, but in at least one case, a local advocate came to argue on NIMBY grounds against Queensway, which would bring pedestrians to their backyard, and for QueensLink, since the passing train would not cause unwanted impact and would serve the area. On net, YIMBYer groups are more pro-QueensLink – for example much of the community at the northern end of the corridor, in Community Board 6, which due to its location on the subway has a more pro-transit and pro-development orientation. But it doesn’t boil down to these class interests pitting professional workers against small business owners, at all. Rather, it’s rather random, boiling down to individual power brokers for Queensway.

What autocrats want

I highlight the randomness of the interest groups for Queensway, because it relates to the broadly autocratic style of some leaders, who the de facto system of government in New York empowers too much. In the 2010s, Andrew Cuomo liked the idea of Queensway, and if he wanted something, anyone who wanted to stay in the good grace of the local power system had to support it. The backward air train to LaGuardia, hated by transit activists in the city from the start, is such an example – while Cuomo was in power opposition was restricted to people outside city and state politics, like the technical advocacy community or Alexandria Ocasio-Cortez. Then Cuomo left office and because nobody really wanted it, this project died. Queensway survives, I think partly because it’s not a multi-billion dollar investment, and partly because some power brokers do like it and have attached themselves to Mayor Eric Adams, such as political operative and lobbyist Travis Terry.

The point of this is not that Adams wants Queensway and therefore it will happen. Rather, it’s that, in a system with a democratic deficit like New York, professional decisions often boil down to which random advocate happens to have the ear of the autocrat. I keep contrasting this with the situation in Berlin, in which bike lanes and pedestrianization have been put on hold and even been reversed under Mayor Kai Wegner (CDU) – but Wegner ran on this agenda in the election and CDU came first, and the pivotal party, SPD, chose to enter a coalition with him and not with more left-wing parties under a known-quantity (and disgraced) leader in Franziska Giffey, whose conservative-for-SPD politics and poor relationship with the left was well-known. I dislike this outcome, but voters knew what they were getting. In contrast, in New York, Adams did not run on any explicit agenda of not building public transit, or even on support for interest groups that oppose transit (again, the Queensway support is more individualized than neighborhood-scale NIMBYs). He just makes abrupt decisions, often sniping the judgment of the city’s own civil service, based on what one favorite asks.

The way forward

In healthy infrastructure construction systems and also in Germany, the planning is not politicized; the yes/no decision on what to build must be made by politicians, but the menu of options with their costs and benefits is prepared by the civil service. In contrast, in the United States, even the choice of which projects get an environmental impact study is politicized; QueensLink advocates are asking for money for an EIS, which in the United States is where planning is done, but even that is stalled politically.

The problem is that the message this behavior by the city and state sends is that New York is too messed up to invest in. Private actors who make investment decisions need some amount of political stability and predictability. A political culture of caprice, in which everyone must constantly follow political gossip to have any idea what the autocratic mayor or governor (or in some countries president or prime minister) will do, or else be swamped by otherwise inexplicable investment decisions, screams “go elsewhere, we don’t want you.” Even turning an EIS into a big political ask screams the same thing: “we can’t do, so merely studying is an achievement by itself and you must pay fealty.”

New York’s current system deters investment, not through taxes or union empowerment, but through opacity and unpredictability. I don’t want to turn the question of one right-of-way in Queens into an existential issue that it is not, but on the margin, stonewalling on QueensLink because some politically connected actor personally wants Queensway reinforces this system that repels investment, whereas treating the EIS as an apolitical step and then based on the results of further planning building it or not based on broad interest agreement signals that New York can and wants to build things. It’s the city’s choice.

The Future of Congestion Pricing in New York

New York just passed congestion pricing, to begin operation on June 30th. The magazine Vital City published an issue dedicated to this policy two days ago; among the articles about it is one by me, about public transportation investments. People should read the entire article; here I’d like to both give more context and discuss some of the other articles in the issue. Much of this comes from what I said to editor Josh Greenman when discussing the pitch for the piece, and how I interpret the other pieces in the same context. The most basic point, for me, is that what matters is if the overall quality of public transit in and around New York is seen to improve in the next 5-10 years. In particular, if congestion pricing is paired with one specific thing (such as a new subway line) and it improves but the rest of the system is seen to decline, then it will not help, and instead people will be cynical about government actions like this and come to oppose further programs and even call for repealing the congestion tax.

The other articles in the issue

There are 10 articles in this issue. One is my own. Another is by Josh, explaining the background to congestion pricing and setting up the other nine articles. The other eight were written by John Surico, Sam Schwartz, Becca Baird-Remba, Austin Celestin, Howard Yaruss, Nicole Gelinas, Vishaan Chakrabarti, and Henry Grabar, and I recommend that people read all of them, for different perspectives.

The general themes the nine of us have covered, not all equally, include,

  • How to use congestion pricing to improve transportation alternatives (me on transit investment, Yaruss on transit fare cuts, Nicole and Chakrabarti on active transportation, Henry on removing parking to improve pedestrian safety).
  • The unpopularity of congestion pricing and what it portends (Surico about polling, Becca about business group opposition, Schwartz on political risk, Yaruss again on why the fare cut is wise); of note, none of the authors are coming out against congestion pricing, just warning that it will need to deliver tangible benefits to remain popular, and Surico is making the point that in London and Stockholm, congestion pricing was unpopular until it took effect, after which it was popular enough that new center-right leadership did not repeal it.
  • Environmental justice issues (Becca and Celestin): my article points out that traffic levels fell within the London congestion zone but not outside it, and Becca and Celestin both point out that the projections in New York are for traffic levels outside the zone not to improve and possibly to worsen, in particular in asthma-stricken Upper Manhattan and the Bronx, Celestin going more deeply into this point and correctly lamenting that not enough transit improvements are intended to go into these areas. The only things I can add to this are that for environmental justice, two good investment targets include a 125th Street subway tunnel extending Second Avenue Subway and battery-electric buses at depots to reduce pollution.
  • Problems with toll evasion (Schwartz and Yaruss): there’s a growing trend of intentional defacement of license plates by the cars’ own drivers, to make them unreadable by traffic camera and avoid paying tolls, which could complicate revenue collection under congestion pricing.

The need for broad success

When discussing my article with Josh, before I wrote it, we talked about the idea of connecting congestion pricing to specific improvements. My lane would be specific transit improvements, like new lines, elevator access at existing stations, and so on, and similarly, Nicole, Henry, Chakrabarti, and Yaruss proposed their own points. But at the same time, it’s not possible to just make one thing work and say “this was funded by congestion pricing.” The entire system has to both be better and look better, the latter since visible revenue collection by the state like congestion pricing or new taxes are always on the chopping block for populist politicians if the state is too unpopular.

The example I gave Josh when we talked was the TGV. The TGV is a clear success as transportation; it is also, unlike congestion pricing, politically safe, in the sense that nobody seriously proposes eliminating it or slowing it down, and the only controversy is about the construction of new, financially marginal lines augmenting the core lilnes. However, the success of the TGV has not prevented populists and people who generally mistrust the state from claiming that things are actually bad; in France, they are often animated by New Left nostalgia for when they could ride slow, cheap trains everywhere, and since they were young then, the long trip times and wait times didn’t matter to them. Such nostalgics complain that regional trains, connecting city pairs where the train has not been competitive with cars since mass motorization and only survived so long as people were too poor to afford cars, are getting worse. Even though ridership in France is up, this specific use case (which by the 1980s was already moribund) is down, leading to mistrust. Unfortunately, while the TGV is politically safe in France, this corner case is used by German rail advocates to argue against the construction of a connected high-speed rail network here, as those corner case trains are better in Germany (while still not carrying much traffic).

The most important conclusion of the story of the TGV is that France needs to keep its high-speed system but adopt German operations, just as Germany needs to adopt French high-speed rail. But in the case of New York, the important lesson to extract is that if the MTA does one thing that I or Nicole or Henry or Chakrabarti or Yaruss called for while neglecting the broad system, people will not be happy. If the MTA builds subway lines with the projected $1 billion a year in revenue, politicians will say “this subway line has been built with congestion pricing revenue,” and then riders will see declines in reliability, frequency, speed, and cleanliness elsewhere and learn to be cynical of the state and oppose further support for the state’s transit operations.

The MTA could split the difference among what we propose. As I mentioned above, I find Celestin’s points about environmental justice compelling, and want to see improvements including new subways in at-risk areas, bus depot electrification to reduce pollution, and commuter rail improvements making it usable by city residents and not just suburbanites (Celestin mentions frequency; to that I’ll add fare integration). Nicole, Henry, and Chakrabarti are proposing street space reallocation, which doesn’t cost much money, but does cost political capital and requires the public to be broadly trusting of the state’s promises on transportation. The problem with doing an all-of-the-above program is that at the end of the day, projected congestion pricing revenue is $1 billion a year and the MTA capital program is $11 billion a year; the new revenue is secondary, and my usual bête noire, construction costs, is primary.

Quick Note: What the Hell is Going on in San Jose?

The BART to San Jose extension always had problems, but somehow things are getting worse. A month and a half ago, it was revealed that the projected cost of the 9.6-kilometer line had risen to $12.2 billion. Every problem that we seemed to identify in our reports about construction costs in New York and Boston appears here as far as I can tell, with the exception of labor, which at least a few years ago showed overstaffing in the Northeastern United States but not elsewhere. In particular, the station and tunnel design maximizes costs – the first link cites Adam Buchbinder on the excessive size of the digs. Unfortunately, the response by the Valley Transportation Authority (VTA) to a question just now about the station shows that not only are the stations insanely expensive, but also not even convenient for passengers (Twitter link, Nitter link).

Cost breakdown

The March 2024 agenda (link, PDF-pp. 488-489) breaks down the costs. The hard costs total $7 billion; the systems : civils ratio is 1:3.5, which is not bad. But the overall hard costs are still extreme. Then on top of them there are soft costs totaling $2.78 billion, or 40% on top of the hard costs. The same percentage for Second Avenue Subway was 21%, and the norm for third-party consultants for the Continental European projects for which we have data (in Italy, Spain, Turkey, and France) is to charge 5-10%. Soft costs should not be this high; if they are, something is deeply wrong with how the agency uses consultants.

Large-diameter tunnel boring machines

The BART to San Jose project has long had two distinct options for tunnels and station: twin bores, and single bore. The twin bore option is conventional construction of two bored tunnels, one for each track, and then stations to be built as dedicated civil construction projects outside the tunnel; this is how most subways are built today. The single bore option is a large-diameter tunnel boring machine (TBM), with the bore large enough to have not just two tracks side by side, but also platforms within the bore, eliminating the need for mined station caverns or for extensive cut-and-cover station digs. Both options cleared environmental reviews; VTA selected the single bore option, which has been controversial.

I’ve written positively about large-diameter TBMs before, and I don’t think I’ve written a full post walking this back. I’ve written about how large-diameter TBMs are inappropriate for San Jose, but the truth is that the method is not treated as a success elsewhere in urban rail, either. This is controversial, and serious engineers still think it works and point to successes in intercity rail, but in urban rail, the problems with building settlement are too serious. The main example of a large-diameter TBM is Barcelona L9/10, which uses the method to avoid having to open up streets under multiple older metro tunnels in Barcelona; it also has high construction costs by Spanish standards (and low costs by non-Spanish ones). In Italy, whose construction costs are also fairly low if not as low as in Madrid, engineers considered using large-diameter TBMs for the sensitive parts of Rome Metro Line C but then rejected that solution as too risky, going for conventional high-cost mined stations instead.

Regardless of the wisdom of doing this in Southern Europe, in San Jose it is stupid. There are wide streets to dig up for cut-and-cover stations. Then, the implementation is bad – the station entryways are too big, whereas Barcelona’s are small elevator banks, and the tunnel bore is wide enough for a platform and two tracks on the same level whereas Barcelona has a narrower bore with stacked platforms.

Thankfully, it is administratively possible to cancel the single bore option, since the twin bore option cleared the environmental reviews as well, and in 2007 was already complete to 65% design (link, PDF-p. 7). Unfortunately, there isn’t much appetite among officials for it. Journalists and advocates are more interested, but the agency seems to stick to its current plans even as their costs are setting non-New York construction cost records.

Is it at least good?

No. Somehow, for this cost, using a method whose primary advantage is that it makes it possible to build a station anywhere at the cost of massively more expensive tunneling, the station at the city’s main train station, named after still-alive Rod Diridon, will not be easily accessible from mainline rail. The walking distance is 400 meters, which has been justified on the grounds that “The decision had to do with impacts and entitlements. It’s also beneficial for the future intermodal station.”

It is, to be clear, not at all beneficial for a future intermodal BART-Caltrain station to require such a long walking distance, provided we take “beneficial” to mean “beneficial for passengers.” It may be beneficial for a Hollywood action sequence to depict characters running through such a space. It is not beneficial for the ordinary users of the station who might be interested in connecting between the two systems. There are 300 meter walks at some transfers in New York, and passengers do whatever they can to avoid them; I’ve taken three-seat rides with shorter transfers to avoid a two-seat ride with a long block transfer, and my behavior is typical of the subway users I know. Transfer corridors of such length are common in Shanghai and are disliked by the system’s users. It’s not the end of the world, but for $1.3 billion/km, I expect better and so should the people who have to pay for this project.

Subway Expansion and Bus Redesign

The ongoing designs for the Interborough Express are making me think about bus redesign again. Before the Transit Costs Project, Eric and I worked on a proposal for a bus redesign in Brooklyn, which sadly was not adopted. The redesign was based on the reality of 2017 – the ridership patterns, the bus speeds, the extent of the system, etc. Since then the subway map has not changed, but IBX stands to change the map, and with it, the buses should change as well.

With our program having produced both the bus redesign proposal and soon a comprehensive proposal for how to change the city’s built-up layout to take advantage of the new line, I should probably say something about how the buses should change. I say I and not we, because so far we don’t have a project under our program for this; for now, this is just a blog post, though one informed by past work on the subject.

Parallel and orthogonal buses

In general, when a new line opens, it reduces demand on parallel bus routes, which it outcompetes, and increases it on orthogonal ones, which feed it. However, what counts as parallel and what counts as orthogonal are not always obvious.

Case in point: when Second Avenue Subway opened at the end of 2016, ridership on the east-west buses between the Upper East and West Sides fell. The new line in theory runs north-south, but it undulates from the Upper East Side to Times Square, where passengers can connect to trains to the Upper West Side and points north; when I lived at 72nd and York and commuted to Columbia by bus and subway in 2009-10, I calculated that if Second Avenue Subway had been open already, a two-seat subway ride with a Times Square connection would have cut my one-way commute from 50 to 37 minutes.

This means that to understand how a new rail line will impact buses, it’s necessary to look beyond just the line itself, and think what it connects to.

For example, note on the above map that the increase in job access at the Flatbush Avenue station, intersecting the Nostrand Avenue Line, is relatively small, and doesn’t have a big north-south footprint along Nostrand. This is because the location already has subway service connecting to Manhattan, a much larger job center than anything IBX would connect to; the buses at the station, the B41 on Flatbush and B44 on Nostrand, already function as connectors to the subway at this point, and are unlikely to acquire more ridership as a result.

In contrast, the stations at Myrtle and Metropolitan are both seen to have a large increase in job access, and in particular a large increase in job access along those two avenues even somewhat away from the stations. On Myrtle, the current buses are the B54 and Q55; the B54 connects to the M train, but it’s one branch, and then the bus continues to Downtown Brooklyn, to which there’s no good subway connection from the future IBX station. The B54 is likely to lose ridership to Downtown Brooklyn but gain it to the new IBX station, and the Q55 is likely to gain in general, as they ferry passengers to a station where they can quickly and with one change go to any number of express lines. Metropolitan has a similar issue – the Q54 already connects to the M, but at least from points west, nobody has any reason to make that connection since it would just double back, whereas with IBX, the Q54 would efficiently connect people to Jackson Heights, and with an additional change to anywhere on the Queens Boulevard and Flushing Lines.

New nodes

Public transit lines serve two functions: to run along a corridor, and to connect nodes. New York usually thinks in terms of corridors, and indeed names nearly all subway lines after the streets they run on (such as a Manhattan avenue) rather than after where they go. But nodes are important as well. Some of that is reflected in the above analysis of the Flatbush-Nostrand Avenue station, currently Brooklyn College on the Nostrand Avenue Line: it really needs to be thought of as a node, and IBX will strengthen it, but not by enough to require running more B41 and B44 buses. In contrast, other nodes will be strengthened enough that bus service increases are warranted.

East New York/Broadway Junction is the biggest standout. East New York’s bus network today is not much of a grid – instead, buses connect outlying areas to the nearest subway station; the bus redesign we did for Brooklyn would make it more of a grid but still follow the logic of feeding the subway wherever it is closest. However, IBX makes Broadway Junction and the Atlantic Avenue station more interesting, which should leads to some changes, turning the new station into more of a node for buses. Buses avoiding this node should instead make sure to stop not just at the subway but also at a new IBX stop, such as Linden.

Jackson Heights is the other. It is a node to some extent today, served by the Q32, Q33, Q47, Q49, Q53, and Q70. But in that general area, the intersection of Woodhaven and Queens Boulevard is an even larger node, and in Queens writ large, the ends of the subway in Jamaica and Flushing are far and away the biggest ones. With IBX, more buses should run to Jackson Heights; for example, all Woodhaven buses, and not just the Q53, should continue along Queens Boulevard and Broadway to reach the station.

Substitutions

In Queens, the street network connecting Jackson Heights with the neighborhoods near the borough line with Brooklyn is not at all conducive for good transit. Buses are usually a good indicator of relative demand along a corridor, but sometimes they aren’t; the situation of IBX is generally one in which they are not, but this is especially bad in Queens. This means that the question of which buses would see demand fall as IBX substitutes for them is even harder than on Second Avenue Subway, the north-south line that efficiently substitutes for east-west buses.

In Brooklyn, I think the answer is relatively straightforward, in that the main crosstown routes, like the B35 on Church, exhibit substitutability. In Queens, it’s harder, and I don’t have concrete answers, only general thoughts that we can turn into a report if there turns out to be demand for it:

  • If a bus has sections along the corridor but also away from it, like the Q18 or Q47, then it should be cut to just connect to the line, in these two case at Jackson Heights.
  • If a bus runs directly between two nodes that could get faster service via a subway-IBX connection, and it doesn’t serve much along the way, then it’s likely to be analogous to the east-west buses across Central Park, and see reduced ridership demand.
  • In general, the routes in Central Queens zigzag so much that IBX is likely to represent a massive improvement in trip times, making such buses less useful.

Frequency in Units of Distance

I have annoying commenters. They nitpick what I say and point out errors in my thinking – or if there are no errors, they take it beyond where I thought it could be taken and find new ways of looking at it. After I wrote about frequency relative to trip length last week, Colin Parker pointed out on the Fediverse that this can be simplified into thinking about frequency not in units of time (trains or buses per hour), but in units of distance (trains or buses per km of route). This post is dedicated to developing this idea on various kinds of transit service, including buses and trains.

The key unit throughout, as Colin points out, is the number of buses available per route, the assumption being that the average trip length is proportional to the average route length. However, this is not a perfect assumption, because then the introduction of network effects changes things – generally in the direction of shorter average trip length, as passengers are likelier to transfer, in turn forcing agencies to run more vehicles on a given route to remain useful. Conversely, timed transfers permit running fewer vehicles, or by the same token more routes with the same resources – but the network had better have a strong node to connect to after a series of vehicle changes, more like the Swiss rail network than like a small American city’s bus network.

Frequency and resources

On a bus network with even frequency across all routes, the following formula governs frequency, as I discussed six years ago:

Daily service hours * average speed per hour = daily trips * network length

When Eric and I proposed our Brooklyn bus redesign, we were working with a service-hour budget of about 10,800 per weekday; status quo as of 2017-8 was 11 km/h, 550 km, and thus 216 daily trips (108 per direction), averaging around a bus per 11 minutes during the daytime, while we were proposing speed up treatments and a redesign to change these figures to 15 km/h, 355 km, and thus 456 daily trips (228 per direction). The six-minute service ideal over 16 hours requires 188 trips per direction; the difference between 188 and 228 is due to higher frequencies on the busiest routes, which need the capacity.

To express this in units of length, we essentially eliminate time from the above dimensional analysis. Daily service hours is a dimensionless quantity: 10,800 hours per weekday means 450 buses circulating at a given time on average, in practice about 570 during the daytime but not many more than 100 buses circulating overnight. If there are 570 buses circulating at a given time, then a 550 km network will average a bus every 1.9 km and a 355 km one will average a bus every 1.25 km. With pre-corona New York bus trips averaging 3.4 km unlinked, a bus every 1.9 km means the maximum headway is a little higher than half the trip time, and a bus every 1.25 km means the maximum headway is a little higher than one third the trip time, independently of speed.

This calculation already illustrates one consequence of looking at frequency in units of distance and not time: your city probably needs to aggressively prune its bus network to limit the wait times relative to overall trip times.

Route length and trip length

On an isolated bus or train route, serving an idealized geography with a destination at its center and isotropic origins along the line, the average trip length is exactly one quarter of the route length. The frequency of service in units of distance should therefore be one eighth of the route length, requiring 16 vehicles to run service plus spares and turnarounds. This is around 18-20 vehicles in isolation, though bear in mind, the 10,800 service hours/day figure for Brooklyn buses above is only for revenue service, and thus already incorporates the margin for turnaround times and deadheads.

Colin points out that where he lives, in Atlanta, bus routes usually have around four vehicles circulating per route at a given time, rather than 16. With the above assumptions, this means that the average wait is twice the average trip time, which goes a long way to explaining why Atlanta’s bus service quality is so poor.

But then, different assumptions of how people travel can reduce the number 16:

  1. If destinations are isotropic, then the average trip length rises from one quarter of the route length to 3/8 of the route length, and then the frequency should be 1.5/8 of the route length, which requires 11 vehicles in revenue service.
  2. If origins are not isotropic, then the average trip length can rise or fall, depending on whether they are likelier to be farther out or closer in. A natural density gradient means origins are disproportionately closer-in, but then in a city with a natural density gradient and only four buses to spare per route, the route is likely to be cut well short of the end of the built-up area. If the end of the route is chosen to be a high-density anchor, then the origins relative to the route itself may be disproportionately farther out. In the limiting case, in which the average trip is half the route length, only eight buses are needed to circulate.

To be clear, this is for a two-tailed route; a one-tailed route, connecting city center at one end to outlying areas at the other, needs half the bus service, but then a city needs twice as many such routes for its network.

The impact of transfers

Transfers can either reduce the required amount of service for it to be worth running or increase it, depending on type. The general rule is that untimed transfers occurring at many points along the line reduce the average unlinked trip and therefore force the city to run more service, while timed transfers occurring at a central node lengthen the effective trip relative to the wait time and therefore permit the city to run less service. In practice, this describes both how existing bus practices work in North America, and even why the Swiss rail network is so enamored with timed connections.

To the point of untimed transfers, their benefit is that there can be very many of them. On an idealized grid – let’s call it Toronto, or maybe Vancouver, or maybe Chicago – every grid corner is a transfer point between an east-west and a north-south route, and passengers can get from anywhere to anywhere. But then they have to wait multiple times; in transit usage statistics, this is seen in low average unlinked trip lengths. New York, as mentioned above, averages 3.4 km bus trips, with a network heavily based on bus-subway transfers; Chicago averages a not much higher 3.9 km. This can sort of work for New York with its okay if not great relative frequency, and I think also for Chicago; Vancouver proper (not so much its suburbs) and Toronto have especially strong all-day frequencies. But weaker transit networks can’t do this – the transfers can still exist but are too onerous. For example, Los Angeles has about the same total bus resources as Chicago but has to spread them across a much larger network, with longer average trip times to boot, and is not meaningfully competitive. The untimed grid, then, is a good feature for transit cities, which have the resources and demand to support the required frequencies.

Not for nothing, rapid transit networks love untimed transfers, and often actively prefer to spread them across multiple stations, to avoid overwhelming the transfer corridors. Subways are only built on routes that are strong enough to have many vehicles circulating, to the point that all but the shortest trips have low ratios of wait to in-vehicle times. They are also usually radial, aiming to get passengers to connect between any pair of stations with just one transfer; Berlin, Paris, and New York are among the main exceptions. These features make untimed transfers tolerable, in ways they aren’t on weaker systems; not for nothing, a city with enough resources for a 100 km bus network and nothing else does not mimic a 100 km subway network.

Timed transfers have the opposite effect as untimed transfers. By definition, a timed transfer means the wait is designed to be very short, ideally zero. At this point, the unlinked trip length ceases to be meaningful – the quantity that should be compared with frequency is the entire trip with all timed transfers included. In particular, lower frequencies may be justifiable, because passengers travel to much more than just the single bus or rail route.

This can be seen in small-city American bus networks, or some night bus networks, albeit not with good quality. It can be seen much more so on transfer-based rail networks like Switzerland’s. The idealized timed transfer network comprises many routes all converging on one node where they are timed to arrive and depart simultaneously, with very short transfers; this is called a knot in German transit planning and a pulse in American transit planning. American networks like this typically run a single bus circulating on each one-tailed route; the average wait works out to be four times longer than the average unlinked trip, and still twice as long as a transfer trip, which helps explain why ridership on such networks is a rounding error, and this system is only used for last-resort transportation in small cities where transit is little more than a soup kitchen or on night bus networks that are hardly more ridden. It would be better to redo such networks, pruning weaker routes to run more service on stronger ones, at least two per one-tailed route and ideally more.

But then the Swiss rail network is very effective, even though it’s based on a similar principle: there’s no way to fill more frequent trains than one every hour to many outlying towns, and even what are midsize cities by Swiss standards can’t support more than a train every half hour, so that many routes have a service offer of two to four vehicles circulating at a given time. However, on this network, the timed transfers are more complex than the idealized pulse – there are many knots with pulses, and they work to connect people to much bigger destinations than could be done with sporadic one-seat rides. A succession of timed connections can get one from a small town in eastern Switzerland to St. Gallen, then Zurich, then Basel, stretching the effective trip to hours, and making the hourly base frequency relatively tolerable. The key feature is that the timed transfers work because while individual links are weak enough to need them, there are some major nodes that they can connect to, often far away from the towns that make the most use of the knot system.

Frequency is Relative

Five years ago, I wrote a blog post about frequency-ridership spirals, mentioning as a side comment that the impact of mass transit frequency on ridership can be lumped together with the trip time. I’d like to develop this point here, and talk about how it affects various kinds of public transportation, including intercity trains.

The rule of thumb I’ve advocated for in ETA reports (for example, on commuter rail) is that the maximum headway should be no more than half the trip time. Untimed transfers reset the clock, since passengers have to wait another time every time they make such a transfer; timed transfers do not, but are rare enough that local public transportation doesn’t usually need to consider them in service planning. Intercity transportation can follow the same rule of thumb, but can also get away with worse frequency since passengers time themselves to arrive shortly before the train does; in particular, hourly trains between cities that are three hours apart are frequent enough that increasing service is valuable only insofar as it provides more capacity, and is unlikely to lead to higher ridership through shorter waits.

Wait and transfer penalties

In the literature on modeling public transportation ridership, it is universal that passengers prefer spending time on board a moving vehicle to waiting for a vehicle, walking to the station, or walking between platforms. This preference is expressed as a factor, called the waiting or transfer penalty. different models have different levels for these penalties; passengers also likely have different penalties depending on circumstances, such as familiarity with the route or how much luggage they’re carrying.

The papers I’ve seen have penalties ranging from 1.75 (in the MTA’s model) to 3 (the higher end cited in Lago-Mayworm-McEnroe). I usually model with 2, in Teulings-Ossokina-de Groot. The factor of 2 has the advantage of consistency with an assumption that passengers don’t have a wait penalty but do assume a worst-case scenario for waits, so that the generalized travel time is equal to the maximum headway plus the in-vehicle travel time.

Update 4-19: I was just alerted to a new study by Yap-Wong-Cats using London ridership, finding an out-of-vehicle penalty factor of 1.94 pre-pandemic and 1.92 post-pandemic.

The impact of frequency relative to trip time

If the elasticity of ridership with respect to the generalized travel time, summing the headway and in-vehicle travel time but not walking time to and from the station, is e, then we can compute the elasticity of ridership with respect to frequency as a fraction of e. If the current headway is a proportion r of the in-vehicle trip time, that is to say a fraction r/(r+1) of the generalized travel time, then the elasticity is er/(r+1).

In Lago-Mayworm-McEnroe, the value of e appears to be 0.8. This means that if r = 0.5, the elasticity of ridership with respect to frequency is 0.267. The paper doesn’t quantify elasticities relative to different levels of r but only relative to absolute frequencies, but 0.267 is within the range it finds for different frequencies, dipping to 0.22 for high-frequency lines. Other papers have different figures of e, often higher in the long run as passengers adjust, but those go up to around 1 or, reasoning backward from a VTPI report, a little higher.

Of notes:

  1. The value of r is not constant across different uses of the same line. A commuter traveling from near the outer end of a subway line to city center faces much lower r than a traveler going a short distance, within city center or within a large outlying neighborhood. In particular, r is generally lower for commutes than for non-commute trips, which is why the latter are more sensitive to frequency.
  2. Systems that rely on extensive transfers can have very high values of r with short in-vehicle trips. New York averages 13.5 minutes per unlinked subway trip, with many trips facing an effective off-peak headway of 10 or even 12 minutes, at which point e is high enough that increasing off-peak frequency could pay for itself through higher paying ridership (see analysis in a blog post and an ETA report). This, again, depends on the type of trip – commuters may pick an apartment or a job based on ease of travel, reducing the need to transfer, but their non-commute trips are usually a collection of irregular trips to various destinations and are likelier to involve a transfer.
  3. The cost of higher frequency depends on mode (it’s higher on buses than trains) and time of day (it’s very low on off-peak trains until it matches peak frequency). Together with points 1 and 2, this argues in favor of raising the off-peak frequency on urban and inner suburban trains, potentially to the point of matching peak frequency. On longer-range commuter trains, the impact of frequency on ridership is lower, and thus the marginal cost may be such that a ratio of peak to off-peak service larger than 1 is desirable.

Intercity trains

The papers I’m citing aim to fit elasticity factors to observed ridership on local and regional public transportation. Intercity rail has its own set of models, with different assumptions. Frequency again matters, but because passengers time themselves to arrive at the departing station shortly before the train leaves, its impact is reduced.

I don’t know the elasticity of intercity rail ridership with respect to frequency; Cascetta-Coppola have the elasticity of ridership with respect to in-vehicle trip time as about -2, while Börjesson has it at -1.5 for business travel and -1 for non-business travel with a rough rule of thumb trying to approximate the impact of frequency. At the level of the sanity check, the low frequency of TGV services is not visible in TGV ridership between the provinces and Paris, compared with Japan (which charges higher fares) and as far as I can tell from a few data points Germany. TGV ridership between the provinces is bad, but that involves trains with service gaps that are much larger than the trip times, reaching six hours between Marseille and Lyon. In contrast, those three-hour gaps in service between Paris and cities three hours away by TGV don’t seem to impact ridership visibly.

What this means is that intercity trains do need a certain baseline frequency. The German system of a train every two hours on every city pair is wise, in light of the typical intercity rail travel distances in a large country with slow trains. Higher frequency is warranted if the cities are bigger and therefore require more service, or if they are closer together in time through either a short geographical distance or higher speeds. New York and Philadelphia are about 1:10 apart by rail, and high-speed rail could cut this to about 45 minutes; half-hourly frequencies in the current situation are sufficient that more service would have a second-order effect, and even with high-speed rail, a train every 15 minutes is more than enough for all purposes except capacity (the current offer is 3-4 trains an hour with irregular spacing). Frequency is freedom, but this depends on trip times; what works for four-station subway trips is not what works for trips between cities 140 km apart, let alone 360 km, and vice versa.

What is Incrementalism, Anyway?

The American conversation about high-speed rail has an internal debate that greatly bothers me, about whether investments should be incremental or not. An interview with the author of a new book about the Northeast Corridor reminded me of this; this is not the focus of the interview, but there was an invocation of incremental vs. full-fat high-speed rail, which doesn’t really mean much. The problem is that the debate over incrementalism can be broken down into separate categories – infrastructure, top speed, planning paradigm, operations, marketing; for example, investment can be mostly on existing tracks or mostly on a new right-of-way, or something in between, but this is a separate questions from whether operations planning should remain similar to how it works today or be thrown away in favor of something entirely new. And what’s more, in some cases the answers to these questions have negative rather than positive correlations – for example, the most aggressively revolutionary answer for infrastructure is putting high-speed trains on dedicated tracks the entire way, including new urban approaches and tunnels at all major cities, but this also implies a deeply conservative operating paradigm with respect to commuter rail.

Instead of talking about incrementalism, it’s better to think in terms of these questions separately. As always, one must start with goals, and then move on to service planning, constraints, and budgets.

Planners who instead start with absolute political demands, like “use preexisting rights-of-way and never carve new ones through private property,” end up failing; California High-Speed Rail began with that demand, as a result of which it planned to use existing freight rail corridors that pass through unserved small towns with grade crossings; this was untenable, so eventually the High-Speed Rail Authority switched to swerving around these unserved towns through farmland, but by then it had made implicit promises to the farmers not to use eminent domain on their land, and when it had to violate the promise, it led to political controversy.

Switzerland

Instead of California’s negative example, we can look to more successful ones, none of which is in an English-speaking country. I bring up Switzerland over and over, because as far as infrastructure goes, it has an incremental intercity rail network – there are only a handful of recently-built high-speed lines and they’re both slow (usually 200 km/h, occasionally 250 km/h) and discontinuous – but its service planning is innovative. This has several features:

Infrastructure-rolling stock-timetable integration

To reduce the costs of infrastructure, Swiss planning integrates the decision of what kind of train to run into the investment plan. To avoid having to spend money on lengthening platforms, Switzerland bought double-deck trains as part of its Rail 2000 plan; double-deckers have their drawbacks, mainly in passenger egress time, but in the case of Switzerland, which has small cities with a surplus of platform tracks, double-deckers are the right choice.

California made many other errors, but its decision to get single-deck trains is correct in its use case: the high-speed trainset market is almost entirely single-deck, and the issue of platform length is not relevant to captive high-speed rail since the number of stations that need high-speed rail service is small and controllable.

Timetable integration is even more important. If the point is to build a rail network for more than just point-to-point trips connecting Zurich, Basel, Bern, and Geneva, then trains have to connect at certain nodes; already in the 1970s, SBB timetables were such that trains arrived at Zurich shortly before the hour every hour and departed on or shortly after the hour. The Rail 2000 plan expanded these timed connections, called Knoten or knots, to more cities, and prioritized speed increases that would enable trains to connect two knots in just less than an hour, to avoid wasting time for passengers and equipment. The slogan is run trains as fast as necessary, not as fast as possible: expensive investment is justifiable to get the trip times between two knots to be a little less than an hour instead of a little more than an hour, but beyond that, it isn’t worth it, because connecting passengers would not benefit.

Tunnels where necessary

The incremental approach of Rail 2000, borne out of a political need to limit construction costs, is sometimes cited by German rail advocates and NIMBYs who assume that Switzerland does not build physical infrastructure. Since the 1980s, when investment in the Zurich S-Bahn and Rail 2000 began, Switzerland has built rail tunnels with gusto, and not just across the Alpine mountain passes for freight but also in and between cities to speed up passenger trains and create more capacity. Relative to population, Switzerland has built more rail tunnel per capita than Germany since the 1980s, let alone France, excluding the trans-Alpine base tunnels.

So overall, this is a program that’s very incremental and conservative when it comes to top speed (200 km/h, rarely 250), and moderately incremental when it comes to infrastructure but does build strategic bypasses, tunnels to allow trains to run as fast as necessary, and capacity improvements. But its planning paradigm and operations are both innovative – Rail 2000 was the first national plan to integrate infrastructure improvements into a knot system, and its successes have been exported into the Netherlands, Austria, and more slowly Germany.

Incrementalism in operations versus in infrastructure

The current trip times between New York and New Haven are 1:37 on intercity trains and 2:02 to 2:08 on commuter trains depending on how many stops they skip between Stamford and New Haven. The technical capability of modern trainsets with modern timetabling is 52 minutes on intercity trains and about 1:17 on commuter trains making the stopping patterns of today’s 2:08 trains.

This requires a single deviation from the right-of-way, at Shell Interlocking just south of New Rochelle, which deviation is calibrated not to damage a historic building close to the track and may not require any building demolitions at all; the main purpose of the Shell Interlocking project is to grade-separate the junction for more capacity, not to plow a right-of-way for fast trains. The impact of this single project on the schedule is hard to quantify but large, because it simplifies timetabling to the point that late trains on one line would not delay others on connecting lines; Switzerland pads the timetable 7%, whereas the TGV network (largely on dedicated tracks, thus relatively insulated from delays) pads 11-14%, and the much more exposed German intercity rail network pads 20-30%. The extent of timetable padding in and around New York is comparable to the German level or even worse; those two-hour trip times include what appears to be about 25 minutes of padding. The related LIRR has what appears to be 32% padding on its Main Line, as of nine years ago.

So in that sense, it’s possible to be fairly conservative with infrastructure, while upending operations completely through tighter scheduling and better trainsets. This should then be reinforced through upending planning completely through providing fewer train stopping patterns, in order to, again, reduce the dependence of different train types on one another.

Is this incremental? It doesn’t involve a lot of physical construction, so in a way, the answer is yes. The equivalent of Shell on the opposite side of New York, Hunter Interlocking, is on the slate of thoroughly incremental improvement projects that New Jersey Transit wishes to invest in, and while it has not been funded yet unfortunately, it is fairly likely to be funded soon.

But it also means throwing out 70 years of how American rail agencies have thought about operations. American agencies separate commuter and intercity rail into different classes of train with price differentiation, rather than letting passengers ride intercity trains within a large metropolitan area for the same price as commuter rail so long as they don’t book a seat. They don’t run repeating timetables all day, but instead aim to provide each suburban station direct service to city center with as few stops as possible at rush hour, with little concern for the off-peak. They certainly don’t integrate infrastructure with rolling stock or timetable decisions.

Incrementalism in different parts of the corridor

The answer to questions of incrementalism does not have to be the same across the country, or even across different parts of the same line. It matters whether the line is easy to bypass, how many passengers are affected, what the cost is, and so on.

Between New York and New Haven, it’s possible to reduce trip times by 7 minutes through various bypasses requiring new rights-of-way, including some tunneling and takings of a number of houses in the low hundreds, generally in wealthy areas. My estimate for how much these bypasses should cost is around $5 billion in total. Is it worth it? Maybe. But it’s not really necessary, and there are lower-hanging fruit elsewhere. (One bypass, west of Stamford, may be desirable – it would save maybe 100 seconds for maybe $500 million, and also provide more capacity on a more constrained section, whereas the other potential bypasses are east of Stamford, where there is much less commuter traffic.)

Between New Haven and Kingston, in contrast, the same $5 billion in bypass would permit a 320 km/h line to run continuously from just east of New Haven to not far south of Providence, with no tunnels, and limited takings. The difference in trip times is 25 minutes. Is that worth it? It should be – it’s a factor of around 1.2 in the New York-Boston trip times, so close to a factor of 1.5 in the projected ridership, which means its value is comparable to spending $15 billion on the difference between this service (including the $5 billion for the bypass) and not having any trains between New York and Boston at all.

South of New York, the more Devin and I look at the infrastructure, the more convinced I am that significant deviations from the right-of-way are unnecessary. The curves on the line are just not that significant, and there are long stretches in New Jersey where the current infrastructure is good and just needs cheap fixes to signals and electrification, not tunnels. Even very tight curves that should be fixed, like Frankford Junction in Philadelphia, are justifiable on the basis of a high benefit-cost ratio but are not make-or-break decisions; getting the timetabling integration right is much more important. This could, again, be construed to mean incrementalism, but we’re also looking at New York-Philadelphia trip times of around 46 minutes where the Acela takes about 1:09 today.

Overall, this program can be described as incremental in the sense of, over than 500 km between Boston and Philadelphia, only proposing 120 km of new right-of-way, plus a handful of junction fixes, switch rebuilds, and curve modifications; curve regradings within the right-of-way can be done by a track-laying machine cheaply and quickly. But it also assumes running trains without any of the many overly conservative assumptions of service in the United States, which used to be enshrined in FRA regulations but no longer are, concerning speed on curves, signaling, rolling stock quality, etc. If the trip time between Boston and Philadelphia is reduced by a factor of 1.8, how incremental is this program, exactly?

Incrementalism in marketing and fares

Finally, there are questions about business planning, marketing, segmentation, and fares. Here, the incremental option depends on what is the prior norm. In France, after market research in advance of the TGV showed that passengers expected the new trains to charge premium fares, SNCF heavily marketed the trains as TGV pour tous, promising to charge the same fares for 260 km/h trains as for 160 km/h ones. Since then, TGV fares have been revamped to resemble airline pricing with fare buckets, but the average fares remain low, around 0.11€/km. But international trains run by companies where SNCF has majority stake, namely Thalys and Eurostar, charge premium fares, going exclusively after the business travel market.

This, too, can be done as a break from the past or as a more incremental system. The American system on the Northeast Corridor is, frankly, bad: there are Acela and Regional trains, branded separately with separate tickets, the Regionals charging around twice as much as European intercity trains per km and the Acelas more than three times as much. Incrementalism means keeping this distinction – but then again, this distinction was not traditional and was instead created for the new Acela trains as they entered into service in 2000. (California High-Speed Rail promised even lower fares than the European average in the 2000s.)

Conclusion

There’s no single meaning to incrementalism in rail investment. Systems that are recognized for avoiding flashy infrastructure can be highly innovative in other ways, as is the case for Rail 2000. At the same time, such systems often do build extensive new infrastructure, just not in ways that makes for sleek maps of high-speed rail infrastructure in the mold of Japan, France, or now China.

What’s more, the question of how much to break from the past in infrastructure, operations, or even marketing depends on both what the past is and what the local geography is. The same planner could come to different conclusions for different lines, or different sections on the same line; it leads to bad planning if the assumption is that the entire line must be turned into 300+ km/h high-speed rail at once or none of it may be, instead of different sections having different solutions. Benefit-cost analyses need to rule the day, with prioritization based on centrally planned criteria of ridership and costs, rather than demands to be incremental or to be bold.